Bayesian Optimization with Expensive Integrands
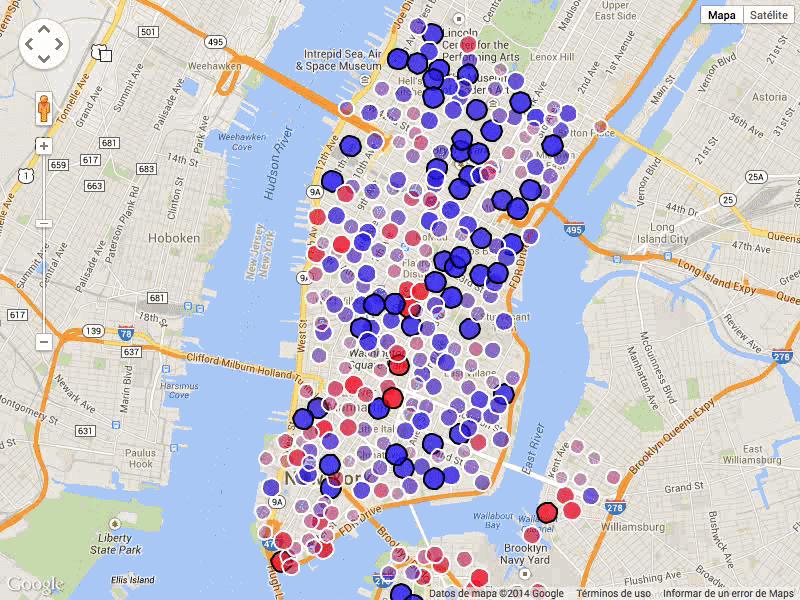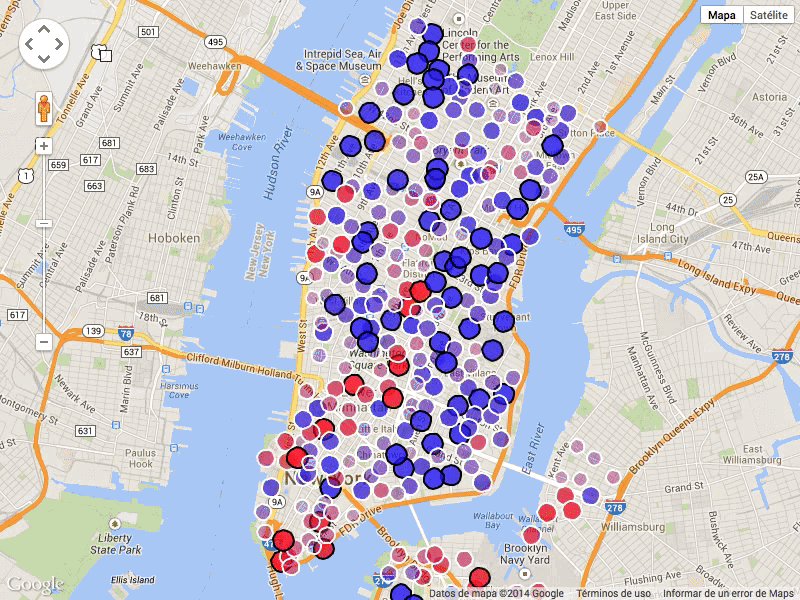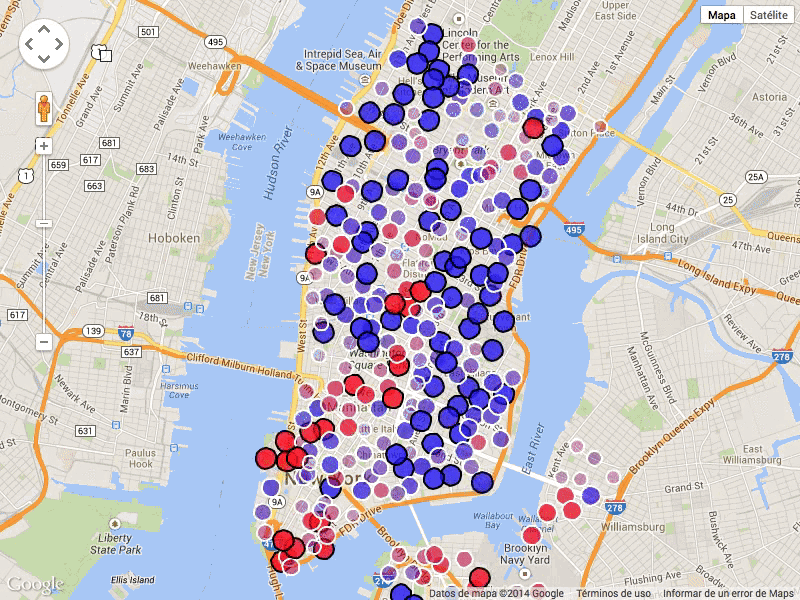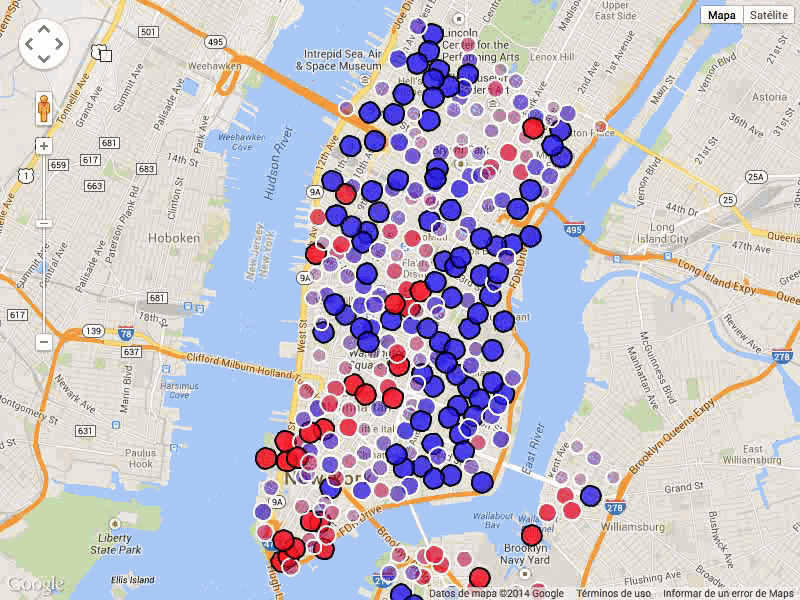
We propose a Bayesian optimization algorithm for objective functions that are sums or integrals of expensive-to-evaluate functions, allowing noisy evaluations. These objective functions arise in multi-task Bayesian optimization for tuning machine learning hyperparameters, optimization via simulation, and sequential design of experiments with random environmental conditions. Our method is average-case optimal by construction when a single evaluation of the integrand remains within our evaluation budget. Achieving this one-step optimality requires solving a challenging value of information optimization problem, for which we provide a novel efficient discretization-free computational method. We also provide consistency proofs for our method in both continuum and discrete finite domains for objective functions that are sums. In numerical experiments comparing against previous state-of-the-art methods, including those that also leverage sum or integral structure, our method performs as well or better across a wide range of problems and offers significant improvements when evaluations are noisy or the integrand varies smoothly in the integrated variables.
PDF Abstract