Boosting Random Forests to Reduce Bias; One-Step Boosted Forest and its Variance Estimate
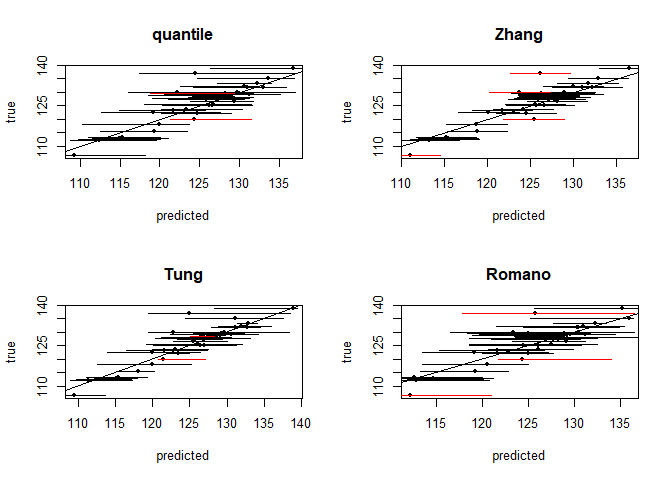
In this paper we propose using the principle of boosting to reduce the bias of a random forest prediction in the regression setting. From the original random forest fit we extract the residuals and then fit another random forest to these residuals. We call the sum of these two random forests a \textit{one-step boosted forest}. We show with simulated and real data that the one-step boosted forest has a reduced bias compared to the original random forest. The paper also provides a variance estimate of the one-step boosted forest by an extension of the infinitesimal Jackknife estimator. Using this variance estimate we can construct prediction intervals for the boosted forest and we show that they have good coverage probabilities. Combining the bias reduction and the variance estimate we show that the one-step boosted forest has a significant reduction in predictive mean squared error and thus an improvement in predictive performance. When applied on datasets from the UCI database, one-step boosted forest performs better than random forest and gradient boosting machine algorithms. Theoretically we can also extend such a boosting process to more than one step and the same principles outlined in this paper can be used to find variance estimates for such predictors. Such boosting will reduce bias even further but it risks over-fitting and also increases the computational burden.
PDF Abstract