Conic Multi-Task Classification
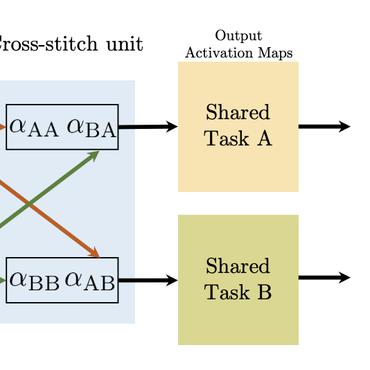
Traditionally, Multi-task Learning (MTL) models optimize the average of task-related objective functions, which is an intuitive approach and which we will be referring to as Average MTL. However, a more general framework, referred to as Conic MTL, can be formulated by considering conic combinations of the objective functions instead; in this framework, Average MTL arises as a special case, when all combination coefficients equal 1. Although the advantage of Conic MTL over Average MTL has been shown experimentally in previous works, no theoretical justification has been provided to date. In this paper, we derive a generalization bound for the Conic MTL method, and demonstrate that the tightest bound is not necessarily achieved, when all combination coefficients equal 1; hence, Average MTL may not always be the optimal choice, and it is important to consider Conic MTL. As a byproduct of the generalization bound, it also theoretically explains the good experimental results of previous relevant works. Finally, we propose a new Conic MTL model, whose conic combination coefficients minimize the generalization bound, instead of choosing them heuristically as has been done in previous methods. The rationale and advantage of our model is demonstrated and verified via a series of experiments by comparing with several other methods.
PDF Abstract