Deep active inference agents using Monte-Carlo methods
Active inference is a Bayesian framework for understanding biological intelligence. The underlying theory brings together perception and action under one single imperative: minimizing free energy. However, despite its theoretical utility in explaining intelligence, computational implementations have been restricted to low-dimensional and idealized situations. In this paper, we present a neural architecture for building deep active inference agents operating in complex, continuous state-spaces using multiple forms of Monte-Carlo (MC) sampling. For this, we introduce a number of techniques, novel to active inference. These include: i) selecting free-energy-optimal policies via MC tree search, ii) approximating this optimal policy distribution via a feed-forward `habitual' network, iii) predicting future parameter belief updates using MC dropouts and, finally, iv) optimizing state transition precision (a high-end form of attention). Our approach enables agents to learn environmental dynamics efficiently, while maintaining task performance, in relation to reward-based counterparts. We illustrate this in a new toy environment, based on the dSprites data-set, and demonstrate that active inference agents automatically create disentangled representations that are apt for modeling state transitions. In a more complex Animal-AI environment, our agents (using the same neural architecture) are able to simulate future state transitions and actions (i.e., plan), to evince reward-directed navigation - despite temporary suspension of visual input. These results show that deep active inference - equipped with MC methods - provides a flexible framework to develop biologically-inspired intelligent agents, with applications in both machine learning and cognitive science.
PDF Abstract NeurIPS 2020 PDF NeurIPS 2020 Abstract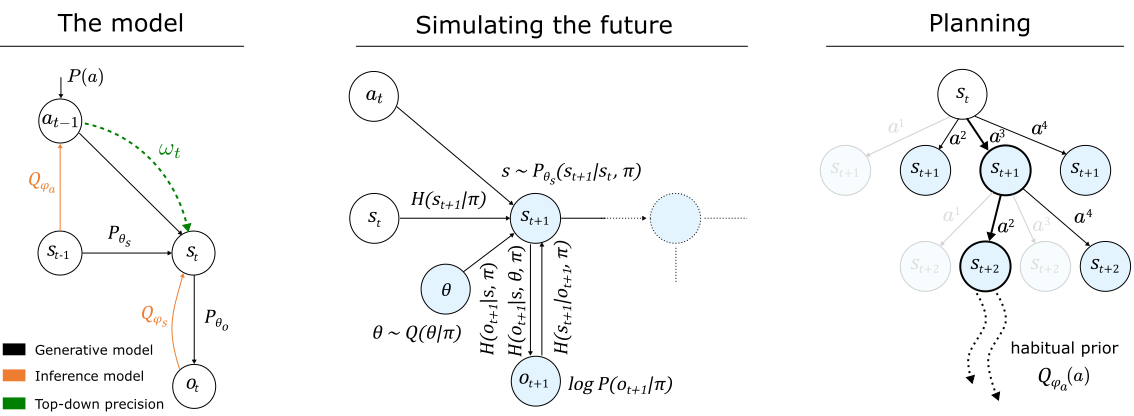
 dSprites
dSprites