Diffusion Models for Causal Discovery via Topological Ordering
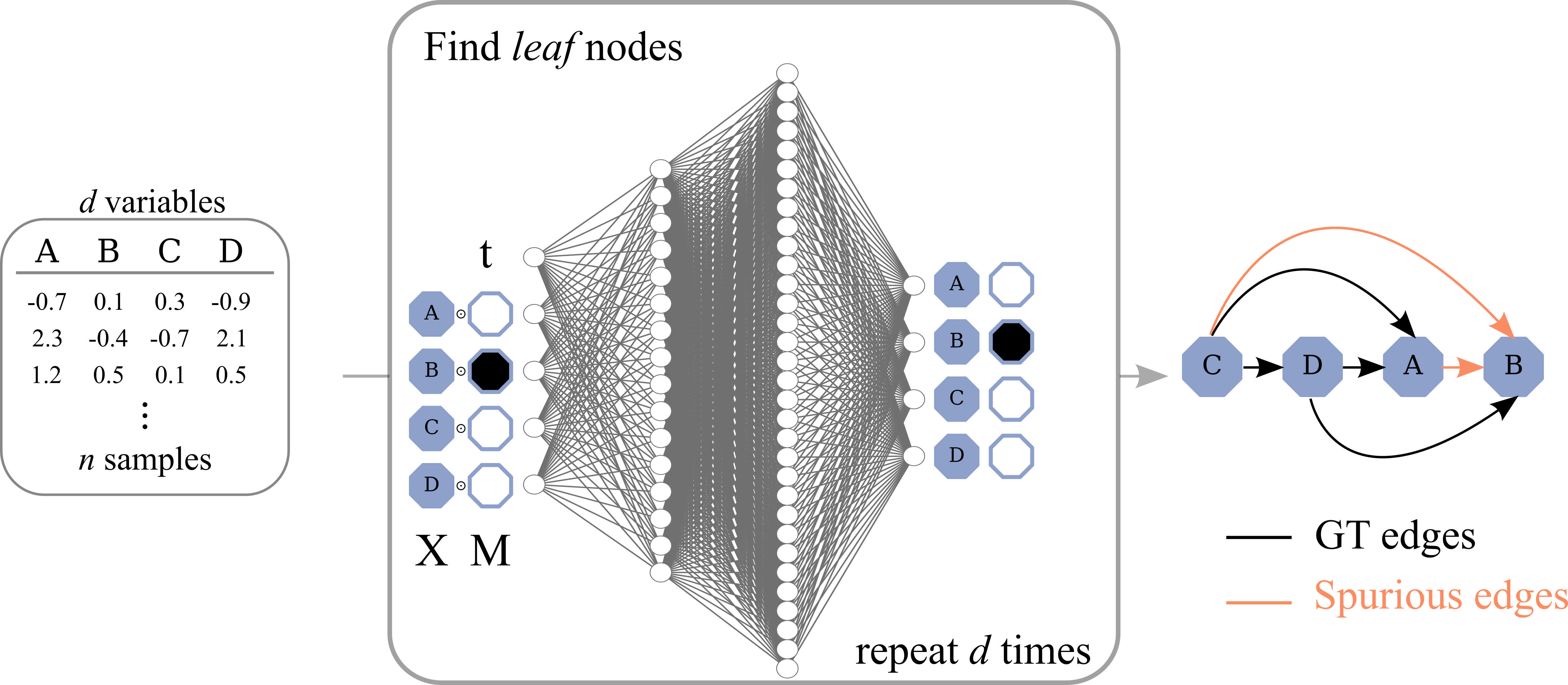
Discovering causal relations from observational data becomes possible with additional assumptions such as considering the functional relations to be constrained as nonlinear with additive noise (ANM). Even with strong assumptions, causal discovery involves an expensive search problem over the space of directed acyclic graphs (DAGs). \emph{Topological ordering} approaches reduce the optimisation space of causal discovery by searching over a permutation rather than graph space. For ANMs, the \emph{Hessian} of the data log-likelihood can be used for finding leaf nodes in a causal graph, allowing its topological ordering. However, existing computational methods for obtaining the Hessian still do not scale as the number of variables and the number of samples increase. Therefore, inspired by recent innovations in diffusion probabilistic models (DPMs), we propose \emph{DiffAN}\footnote{Implementation is available at \url{https://github.com/vios-s/DiffAN} .}, a topological ordering algorithm that leverages DPMs for learning a Hessian function. We introduce theory for updating the learned Hessian without re-training the neural network, and we show that computing with a subset of samples gives an accurate approximation of the ordering, which allows scaling to datasets with more samples and variables. We show empirically that our method scales exceptionally well to datasets with up to $500$ nodes and up to $10^5$ samples while still performing on par over small datasets with state-of-the-art causal discovery methods. Implementation is available at https://github.com/vios-s/DiffAN .
PDF Abstract