$\ell_\infty$-Robustness and Beyond: Unleashing Efficient Adversarial Training
Neural networks are vulnerable to adversarial attacks: adding well-crafted, imperceptible perturbations to their input can modify their output. Adversarial training is one of the most effective approaches in training robust models against such attacks. However, it is much slower than vanilla training of neural networks since it needs to construct adversarial examples for the entire training data at every iteration, hampering its effectiveness. Recently, Fast Adversarial Training (FAT) was proposed that can obtain robust models efficiently. However, the reasons behind its success are not fully understood, and more importantly, it can only train robust models for $\ell_\infty$-bounded attacks as it uses FGSM during training. In this paper, by leveraging the theory of coreset selection, we show how selecting a small subset of training data provides a general, more principled approach toward reducing the time complexity of robust training. Unlike existing methods, our approach can be adapted to a wide variety of training objectives, including TRADES, $\ell_p$-PGD, and Perceptual Adversarial Training (PAT). Our experimental results indicate that our approach speeds up adversarial training by 2-3 times while experiencing a slight reduction in the clean and robust accuracy.
PDF Abstract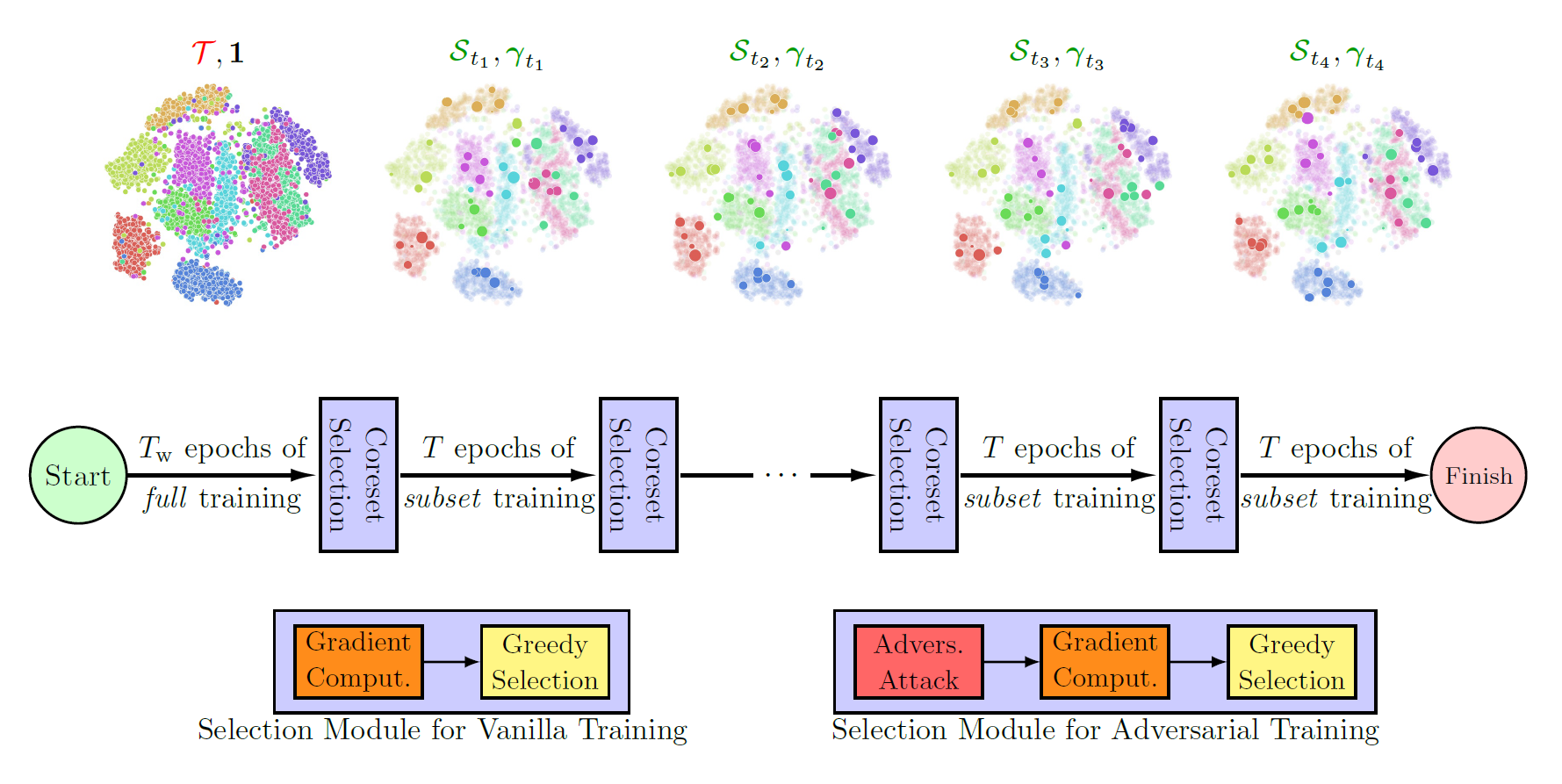

 CIFAR-10
CIFAR-10
 SVHN
SVHN