Gradient Gating for Deep Multi-Rate Learning on Graphs
We present Gradient Gating (G$^2$), a novel framework for improving the performance of Graph Neural Networks (GNNs). Our framework is based on gating the output of GNN layers with a mechanism for multi-rate flow of message passing information across nodes of the underlying graph. Local gradients are harnessed to further modulate message passing updates. Our framework flexibly allows one to use any basic GNN layer as a wrapper around which the multi-rate gradient gating mechanism is built. We rigorously prove that G$^2$ alleviates the oversmoothing problem and allows the design of deep GNNs. Empirical results are presented to demonstrate that the proposed framework achieves state-of-the-art performance on a variety of graph learning tasks, including on large-scale heterophilic graphs.
PDF Abstract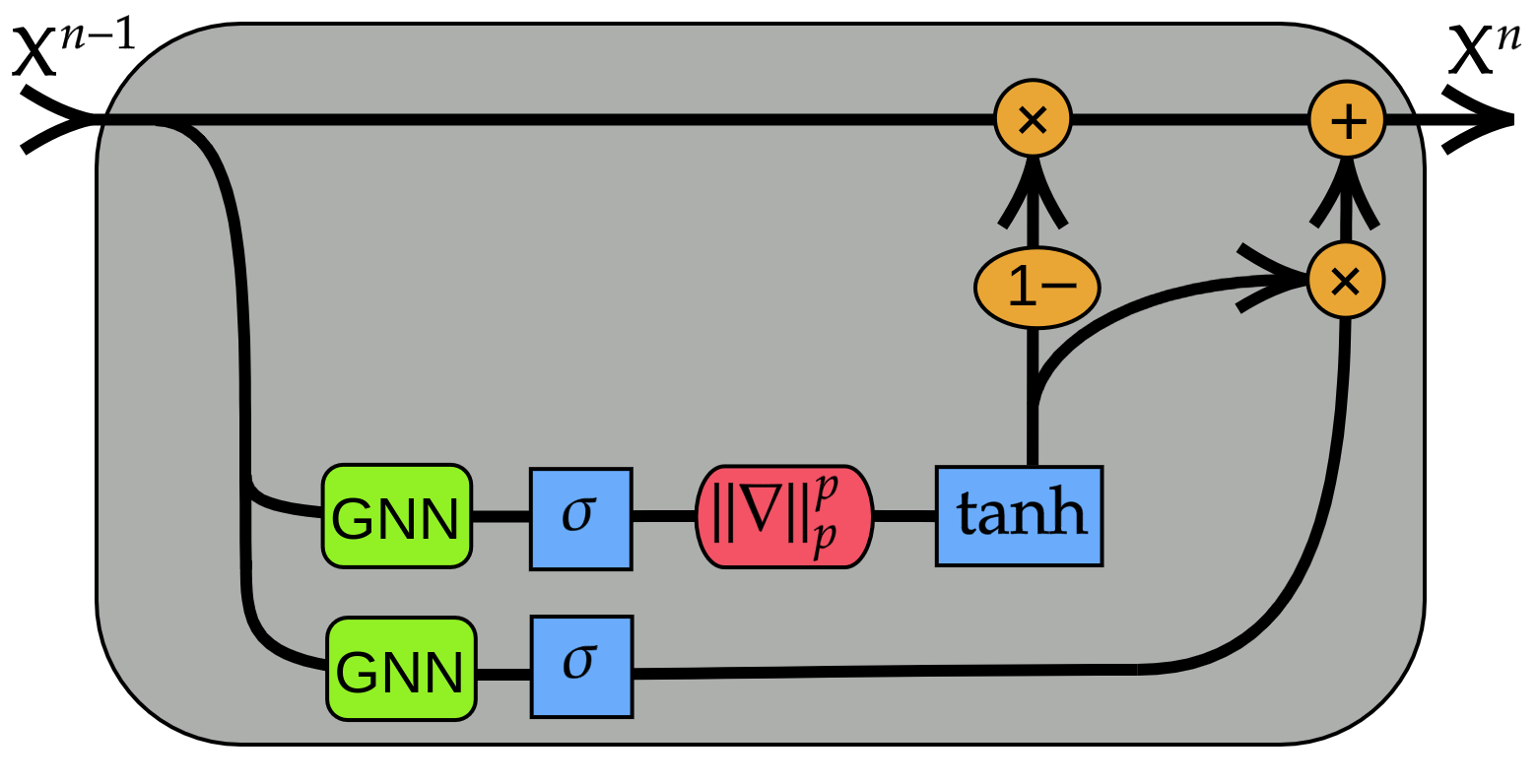






 Wiki Squirrel
Wiki Squirrel
