GraphGAN: Graph Representation Learning with Generative Adversarial Nets
The goal of graph representation learning is to embed each vertex in a graph into a low-dimensional vector space. Existing graph representation learning methods can be classified into two categories: generative models that learn the underlying connectivity distribution in the graph, and discriminative models that predict the probability of edge existence between a pair of vertices. In this paper, we propose GraphGAN, an innovative graph representation learning framework unifying above two classes of methods, in which the generative model and discriminative model play a game-theoretical minimax game. Specifically, for a given vertex, the generative model tries to fit its underlying true connectivity distribution over all other vertices and produces "fake" samples to fool the discriminative model, while the discriminative model tries to detect whether the sampled vertex is from ground truth or generated by the generative model. With the competition between these two models, both of them can alternately and iteratively boost their performance. Moreover, when considering the implementation of generative model, we propose a novel graph softmax to overcome the limitations of traditional softmax function, which can be proven satisfying desirable properties of normalization, graph structure awareness, and computational efficiency. Through extensive experiments on real-world datasets, we demonstrate that GraphGAN achieves substantial gains in a variety of applications, including link prediction, node classification, and recommendation, over state-of-the-art baselines.
PDF Abstract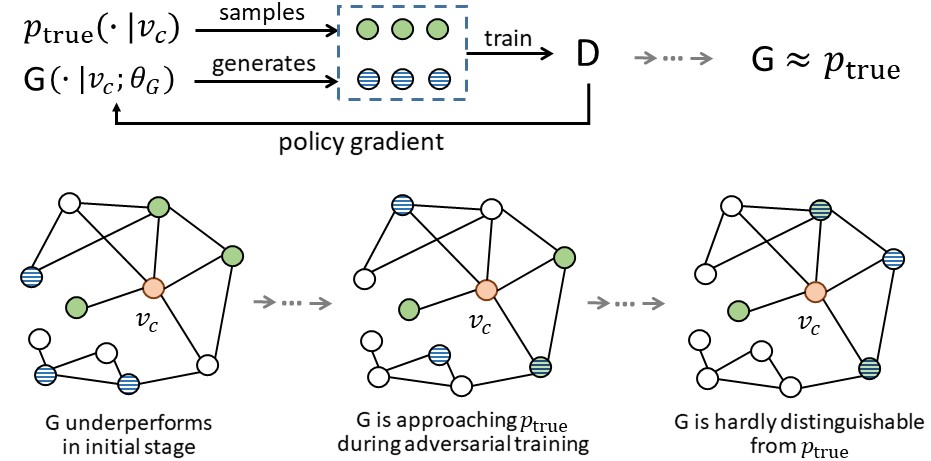






 Eximtradedata
Eximtradedata
