Learned Proximal Networks for Quantitative Susceptibility Mapping
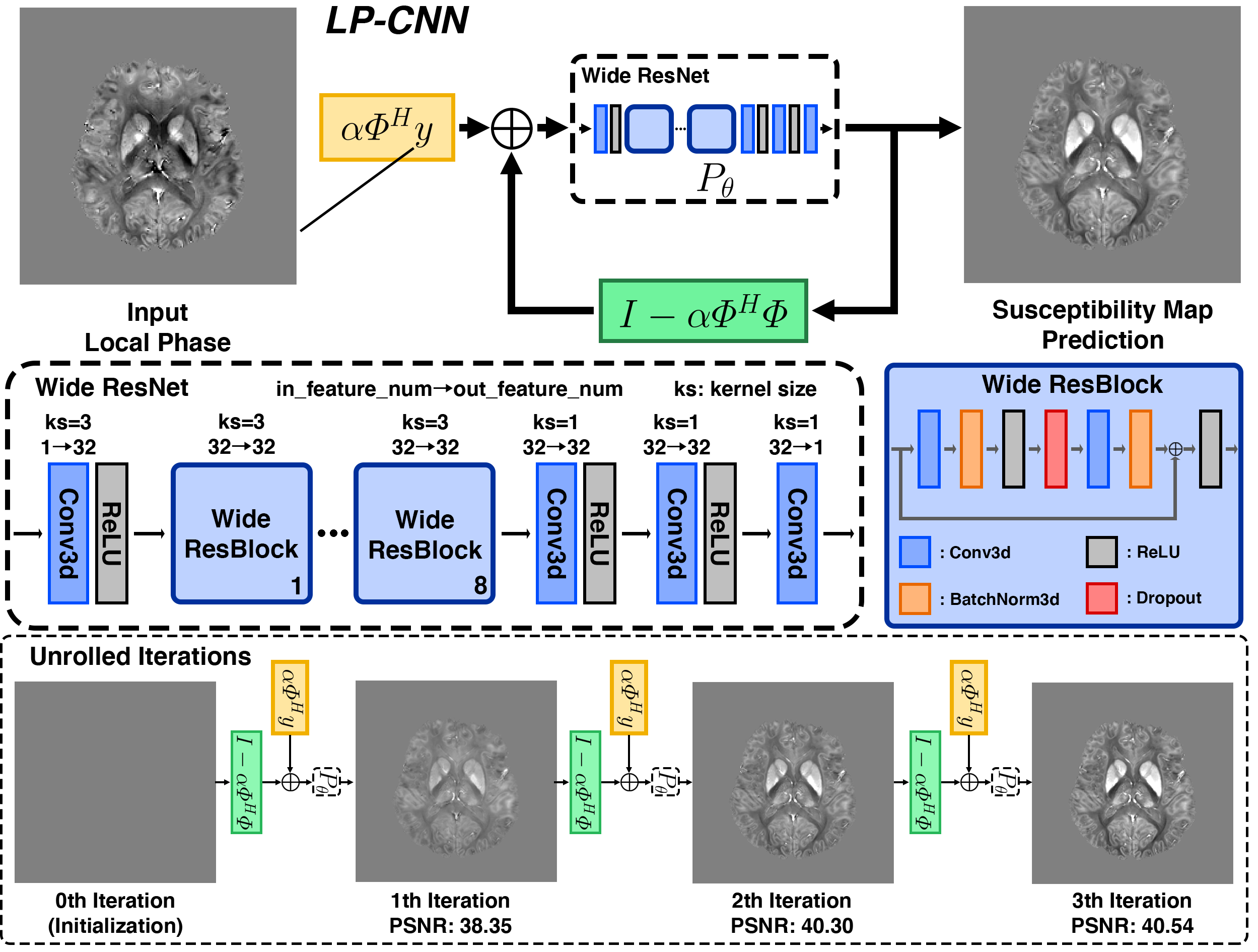
Quantitative Susceptibility Mapping (QSM) estimates tissue magnetic susceptibility distributions from Magnetic Resonance (MR) phase measurements by solving an ill-posed dipole inversion problem. Conventional single orientation QSM methods usually employ regularization strategies to stabilize such inversion, but may suffer from streaking artifacts or over-smoothing. Multiple orientation QSM such as calculation of susceptibility through multiple orientation sampling (COSMOS) can give well-conditioned inversion and an artifact free solution but has expensive acquisition costs. On the other hand, Convolutional Neural Networks (CNN) show great potential for medical image reconstruction, albeit often with limited interpretability. Here, we present a Learned Proximal Convolutional Neural Network (LP-CNN) for solving the ill-posed QSM dipole inversion problem in an iterative proximal gradient descent fashion. This approach combines the strengths of data-driven restoration priors and the clear interpretability of iterative solvers that can take into account the physical model of dipole convolution. During training, our LP-CNN learns an implicit regularizer via its proximal, enabling the decoupling between the forward operator and the data-driven parameters in the reconstruction algorithm. More importantly, this framework is believed to be the first deep learning QSM approach that can naturally handle an arbitrary number of phase input measurements without the need for any ad-hoc rotation or re-training. We demonstrate that the LP-CNN provides state-of-the-art reconstruction results compared to both traditional and deep learning methods while allowing for more flexibility in the reconstruction process.
PDF Abstract