Learning Generalized Quasi-Geostrophic Models Using Deep Neural Numerical Models
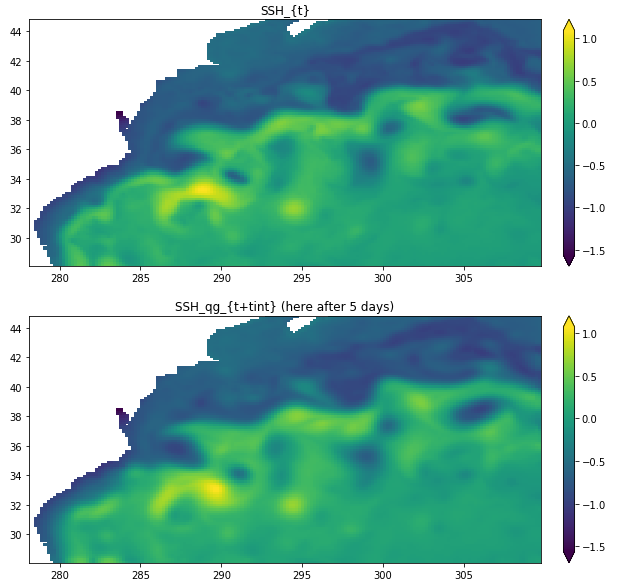
We introduce a new strategy designed to help physicists discover hidden laws governing dynamical systems. We propose to use machine learning automatic differentiation libraries to develop hybrid numerical models that combine components based on prior physical knowledge with components based on neural networks. In these architectures, named Deep Neural Numerical Models (DNNMs), the neural network components are used as building-blocks then deployed for learning hidden variables of underlying physical laws governing dynamical systems. In this paper, we illustrate an application of DNNMs to upper ocean dynamics, more precisely the dynamics of a sea surface tracer, the Sea Surface Height (SSH). We develop an advection-based fully differentiable numerical scheme, where parts of the computations can be replaced with learnable ConvNets, and make connections with the single-layer Quasi-Geostrophic (QG) model, a baseline theory in physical oceanography developed decades ago.
PDF Abstract