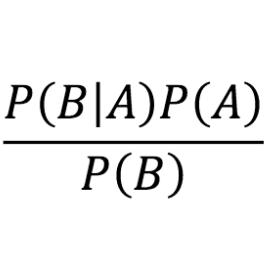Locally Learned Synaptic Dropout for Complete Bayesian Inference
The Bayesian brain hypothesis postulates that the brain accurately operates on statistical distributions according to Bayes' theorem. The random failure of presynaptic vesicles to release neurotransmitters may allow the brain to sample from posterior distributions of network parameters, interpreted as epistemic uncertainty. It has not been shown previously how random failures might allow networks to sample from observed distributions, also known as aleatoric or residual uncertainty. Sampling from both distributions enables probabilistic inference, efficient search, and creative or generative problem solving. We demonstrate that under a population-code based interpretation of neural activity, both types of distribution can be represented and sampled with synaptic failure alone. We first define a biologically constrained neural network and sampling scheme based on synaptic failure and lateral inhibition. Within this framework, we derive drop-out based epistemic uncertainty, then prove an analytic mapping from synaptic efficacy to release probability that allows networks to sample from arbitrary, learned distributions represented by a receiving layer. Second, our result leads to a local learning rule by which synapses adapt their release probabilities. Our result demonstrates complete Bayesian inference, related to the variational learning method of dropout, in a biologically constrained network using only locally-learned synaptic failure rates.
PDF Abstract