Neural Graph Reasoning: Complex Logical Query Answering Meets Graph Databases
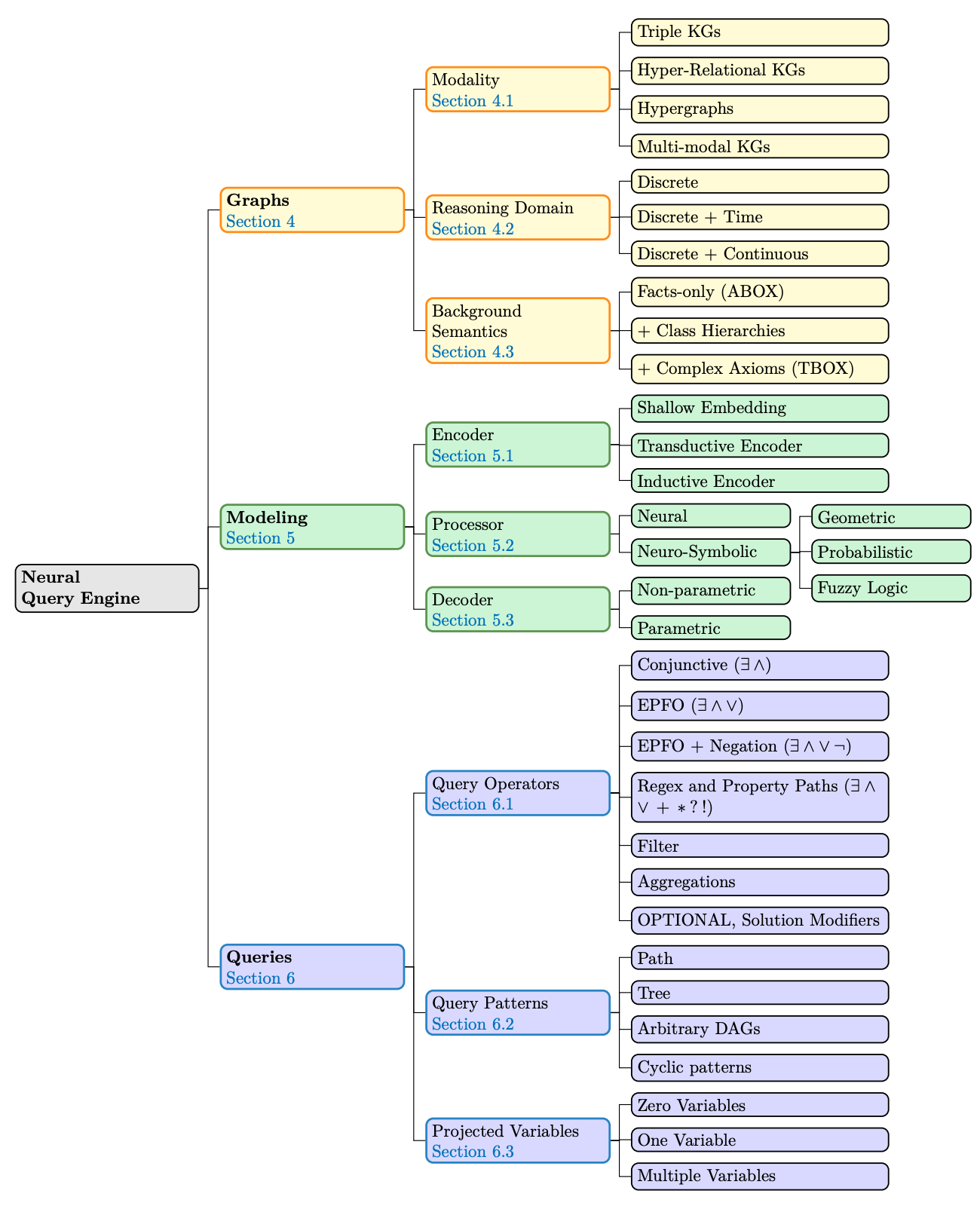
Complex logical query answering (CLQA) is a recently emerged task of graph machine learning that goes beyond simple one-hop link prediction and solves a far more complex task of multi-hop logical reasoning over massive, potentially incomplete graphs in a latent space. The task received a significant traction in the community; numerous works expanded the field along theoretical and practical axes to tackle different types of complex queries and graph modalities with efficient systems. In this paper, we provide a holistic survey of CLQA with a detailed taxonomy studying the field from multiple angles, including graph types (modality, reasoning domain, background semantics), modeling aspects (encoder, processor, decoder), supported queries (operators, patterns, projected variables), datasets, evaluation metrics, and applications. Refining the CLQA task, we introduce the concept of Neural Graph Databases (NGDBs). Extending the idea of graph databases (graph DBs), NGDB consists of a Neural Graph Storage and a Neural Graph Engine. Inside Neural Graph Storage, we design a graph store, a feature store, and further embed information in a latent embedding store using an encoder. Given a query, Neural Query Engine learns how to perform query planning and execution in order to efficiently retrieve the correct results by interacting with the Neural Graph Storage. Compared with traditional graph DBs, NGDBs allow for a flexible and unified modeling of features in diverse modalities using the embedding store. Moreover, when the graph is incomplete, they can provide robust retrieval of answers which a normal graph DB cannot recover. Finally, we point out promising directions, unsolved problems and applications of NGDB for future research.
PDF Abstract