Neural SDEs as Infinite-Dimensional GANs
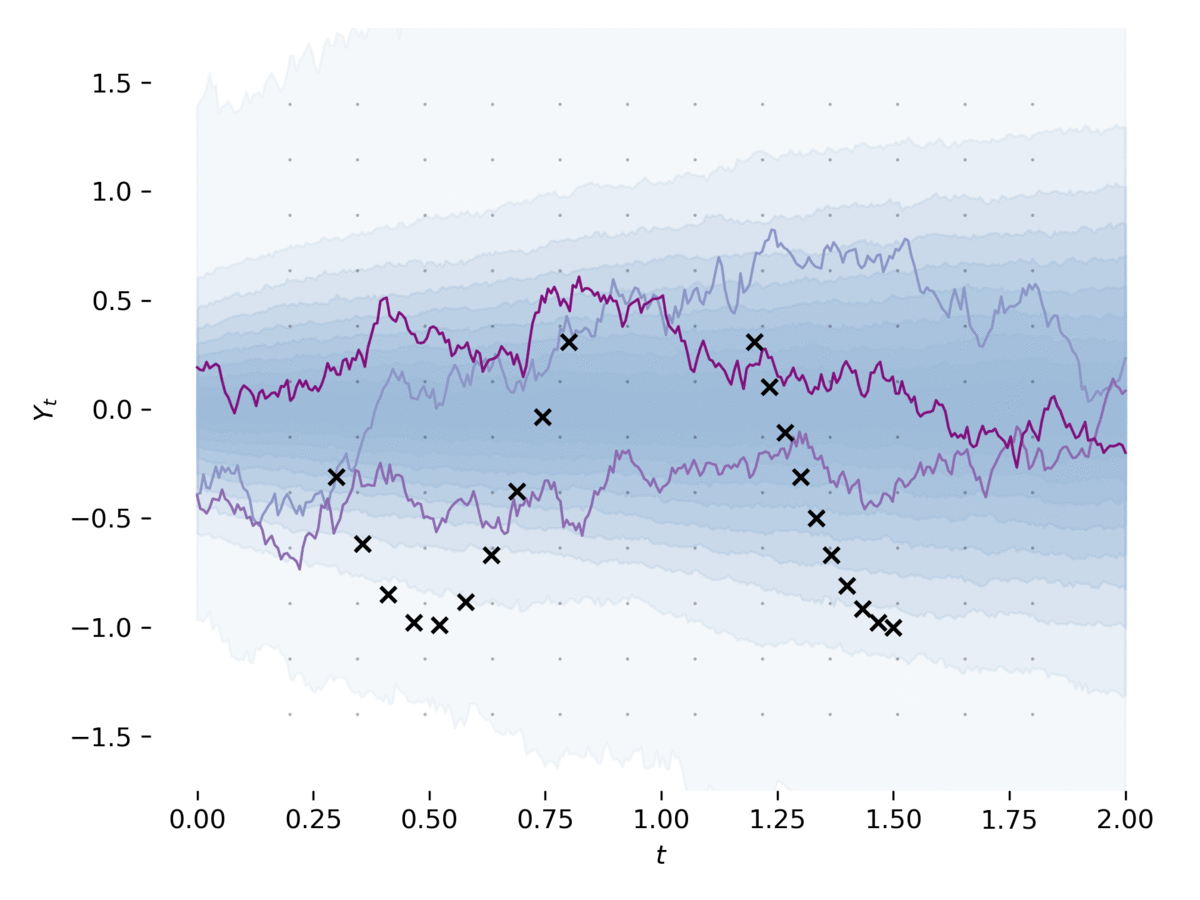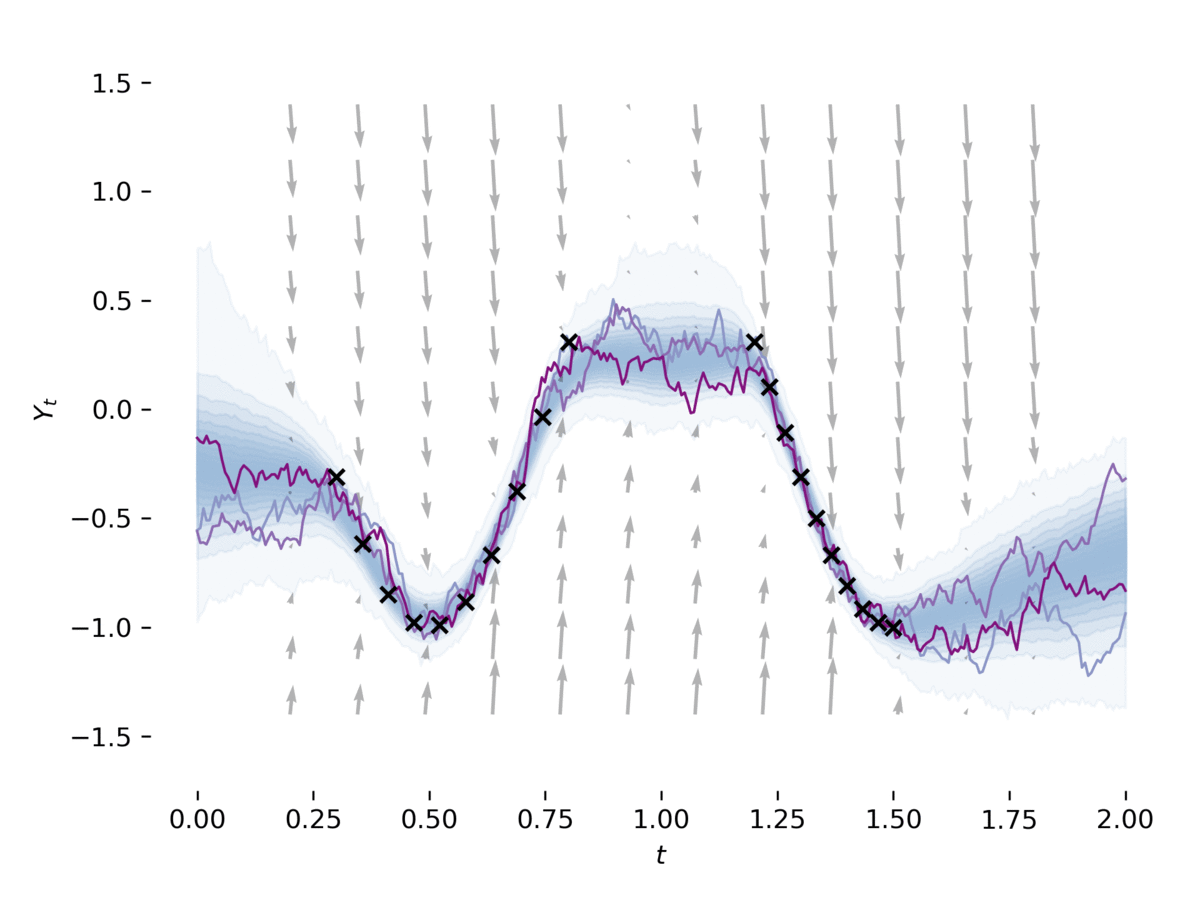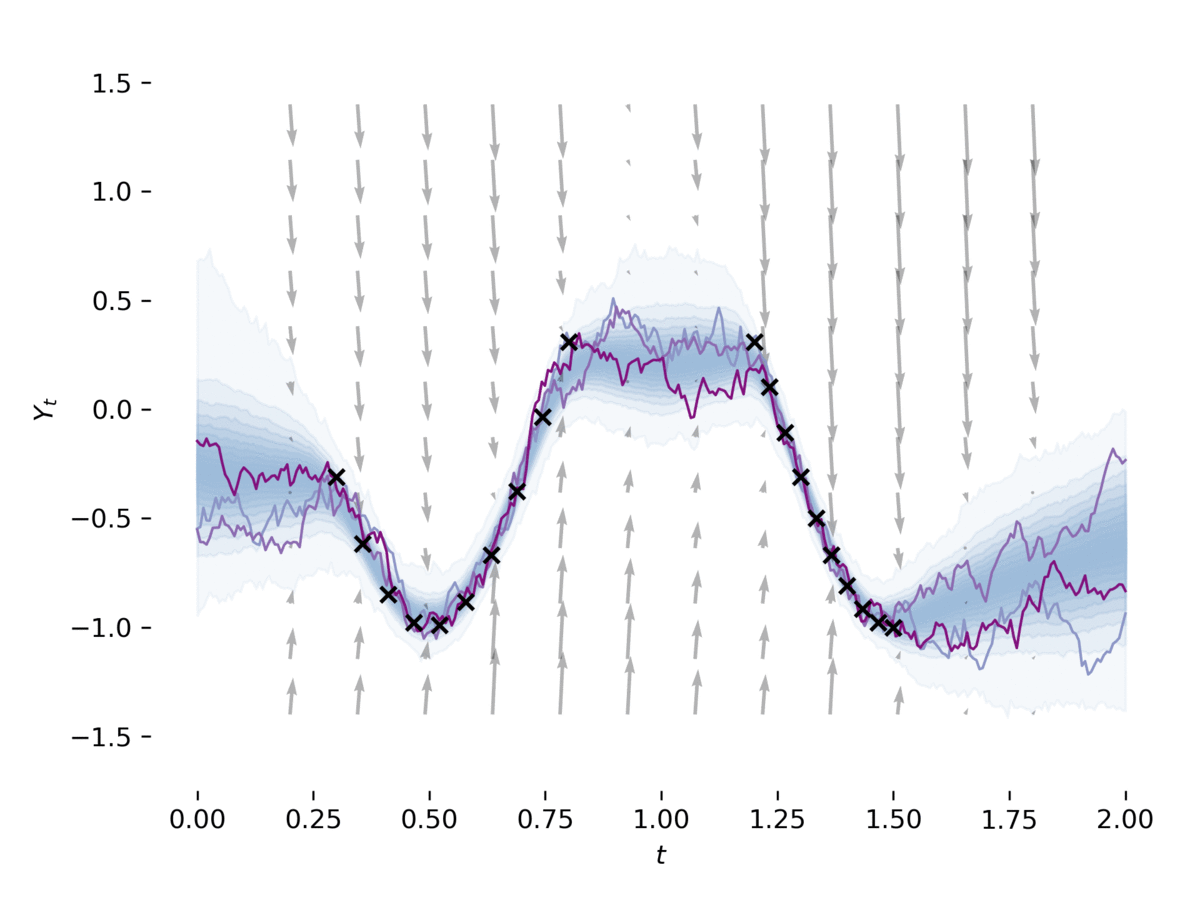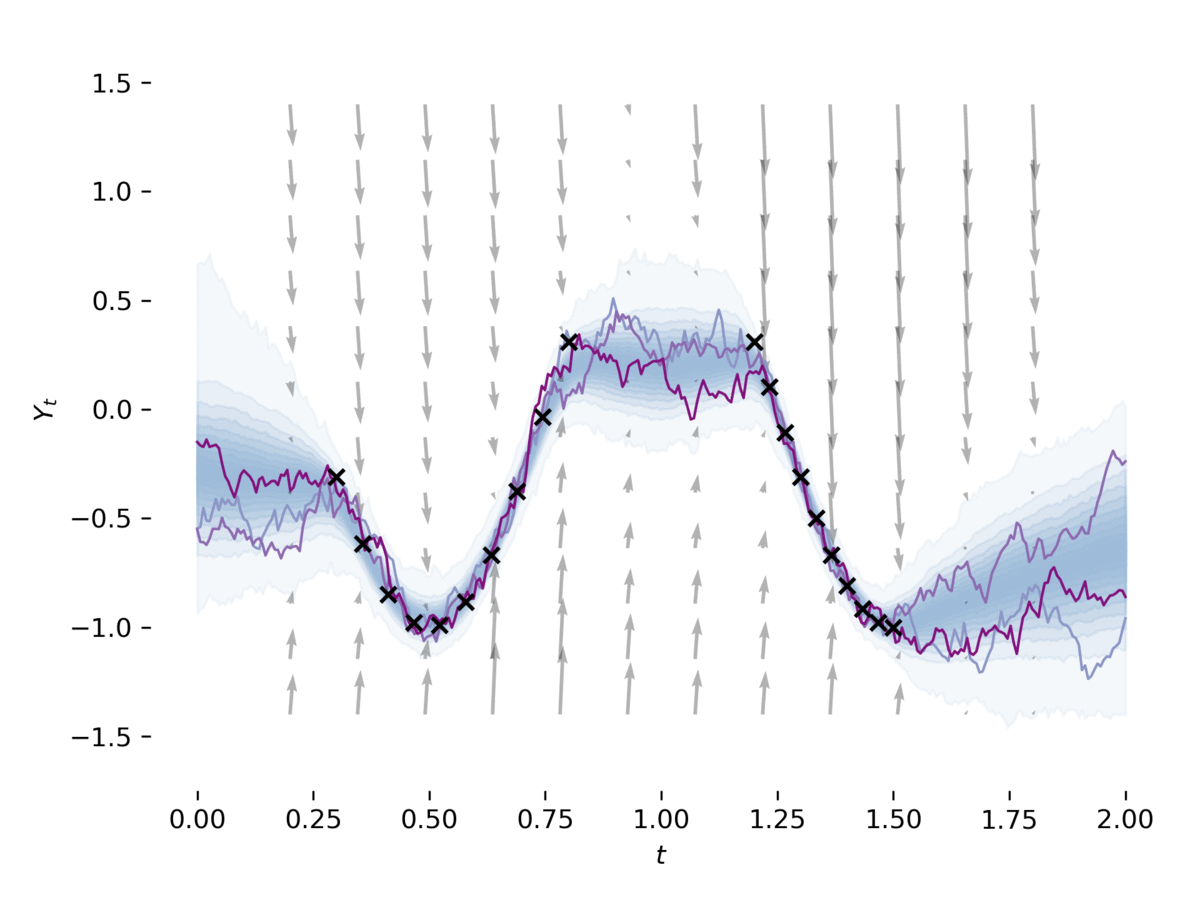
Stochastic differential equations (SDEs) are a staple of mathematical modelling of temporal dynamics. However, a fundamental limitation has been that such models have typically been relatively inflexible, which recent work introducing Neural SDEs has sought to solve. Here, we show that the current classical approach to fitting SDEs may be approached as a special case of (Wasserstein) GANs, and in doing so the neural and classical regimes may be brought together. The input noise is Brownian motion, the output samples are time-evolving paths produced by a numerical solver, and by parameterising a discriminator as a Neural Controlled Differential Equation (CDE), we obtain Neural SDEs as (in modern machine learning parlance) continuous-time generative time series models. Unlike previous work on this problem, this is a direct extension of the classical approach without reference to either prespecified statistics or density functions. Arbitrary drift and diffusions are admissible, so as the Wasserstein loss has a unique global minima, in the infinite data limit any SDE may be learnt. Example code has been made available as part of the \texttt{torchsde} repository.
PDF Abstract