Node Embedding with Adaptive Similarities for Scalable Learning over Graphs
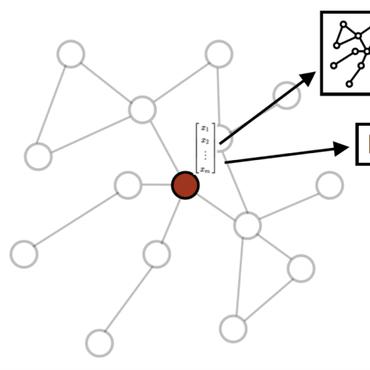
Node embedding is the task of extracting informative and descriptive features over the nodes of a graph. The importance of node embeddings for graph analytics, as well as learning tasks such as node classification, link prediction and community detection, has led to increased interest on the problem leading to a number of recent advances. Much like PCA in the feature domain, node embedding is an inherently \emph{unsupervised} task; in lack of metadata used for validation, practical methods may require standardization and limiting the use of tunable hyperparameters. Finally, node embedding methods are faced with maintaining scalability in the face of large-scale real-world graphs of ever-increasing sizes. In the present work, we propose an adaptive node embedding framework that adjusts the embedding process to a given underlying graph, in a fully unsupervised manner. To achieve this, we adopt the notion of a tunable node similarity matrix that assigns weights on paths of different length. The design of the multilength similarities ensures that the resulting embeddings also inherit interpretable spectral properties. The proposed model is carefully studied, interpreted, and numerically evaluated using stochastic block models. Moreover, an algorithmic scheme is proposed for training the model parameters effieciently and in an unsupervised manner. We perform extensive node classification, link prediction, and clustering experiments on many real world graphs from various domains, and compare with state-of-the-art scalable and unsupervised node embedding alternatives. The proposed method enjoys superior performance in many cases, while also yielding interpretable information on the underlying structure of the graph.
PDF Abstract