Positional Games and QBF: A Polished Encoding
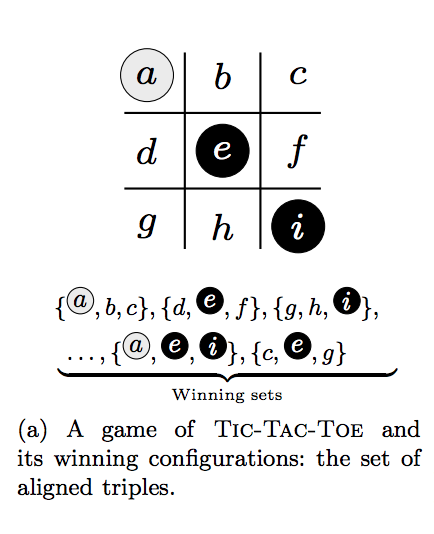
Positional games are a mathematical class of two-player games comprising Tic-tac-toe and its generalizations. We propose a novel encoding of these games into Quantified Boolean Formulas (QBFs) such that a game instance admits a winning strategy for the first player if and only if the corresponding formula is true. Our approach improves over previous QBF encodings of games in multiple ways. First, it is generic and lets us encode other positional games, such as Hex. Second, the structural properties of positional games, together with careful treatment of illegal moves, let us generate more compact instances that can be solved faster by state-of-the-art QBF solvers. We establish the latter fact through extensive experiments. Finally, the compactness of our new encoding makes it feasible to translate realistic game problems. We identify a few such problems of historical significance and put them forward to the QBF community as milestones of increasing difficulty.
PDF Abstract