Resolution learning in deep convolutional networks using scale-space theory
Resolution in deep convolutional neural networks (CNNs) is typically bounded by the receptive field size through filter sizes, and subsampling layers or strided convolutions on feature maps. The optimal resolution may vary significantly depending on the dataset. Modern CNNs hard-code their resolution hyper-parameters in the network architecture which makes tuning such hyper-parameters cumbersome. We propose to do away with hard-coded resolution hyper-parameters and aim to learn the appropriate resolution from data. We use scale-space theory to obtain a self-similar parametrization of filters and make use of the N-Jet: a truncated Taylor series to approximate a filter by a learned combination of Gaussian derivative filters. The parameter sigma of the Gaussian basis controls both the amount of detail the filter encodes and the spatial extent of the filter. Since sigma is a continuous parameter, we can optimize it with respect to the loss. The proposed N-Jet layer achieves comparable performance when used in state-of-the art architectures, while learning the correct resolution in each layer automatically. We evaluate our N-Jet layer on both classification and segmentation, and we show that learning sigma is especially beneficial for inputs at multiple sizes.
PDF Abstract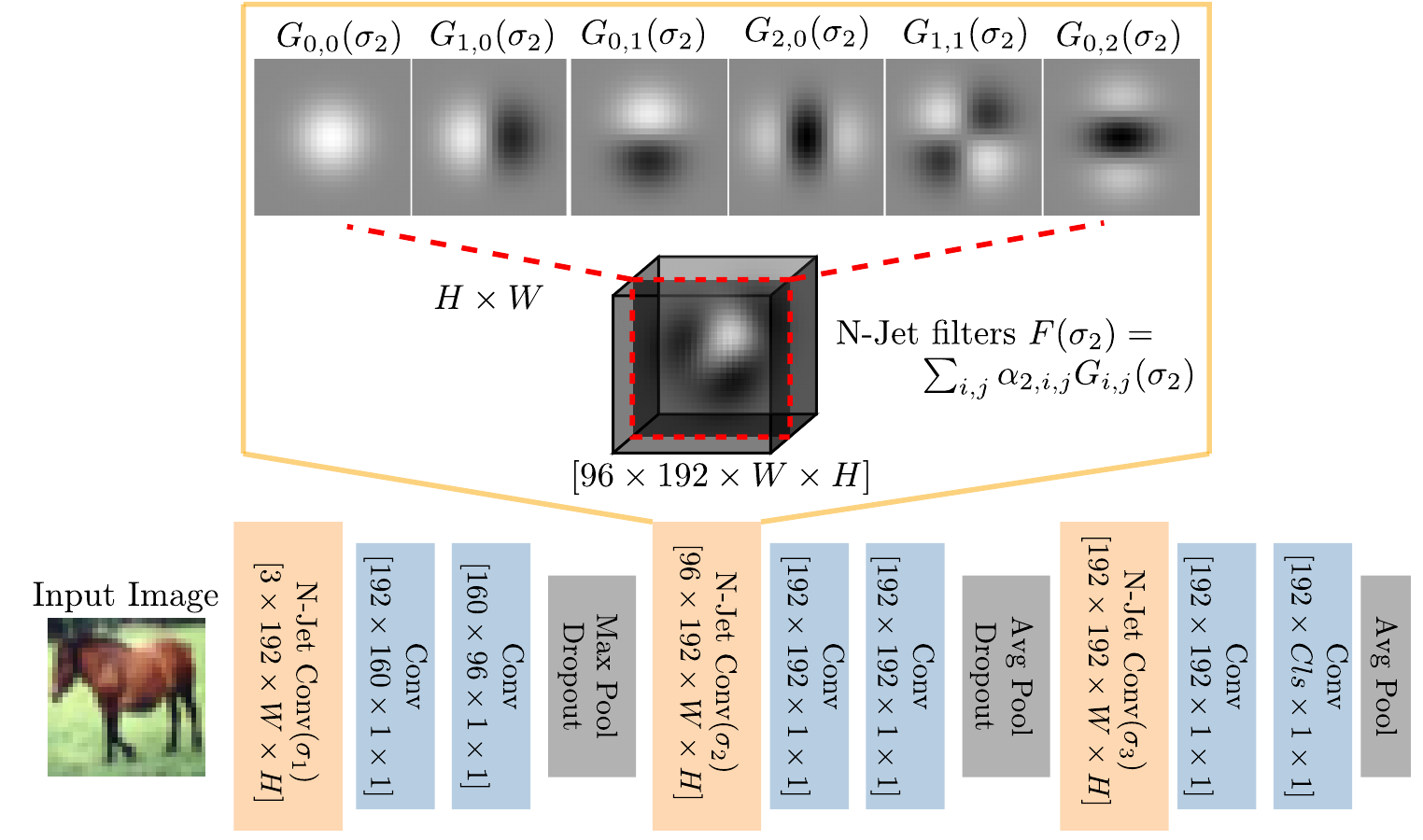

 CIFAR-10
CIFAR-10
 CIFAR-100
CIFAR-100
 SVHN
SVHN
 Fashion-MNIST
Fashion-MNIST