Stable Architectures for Deep Neural Networks
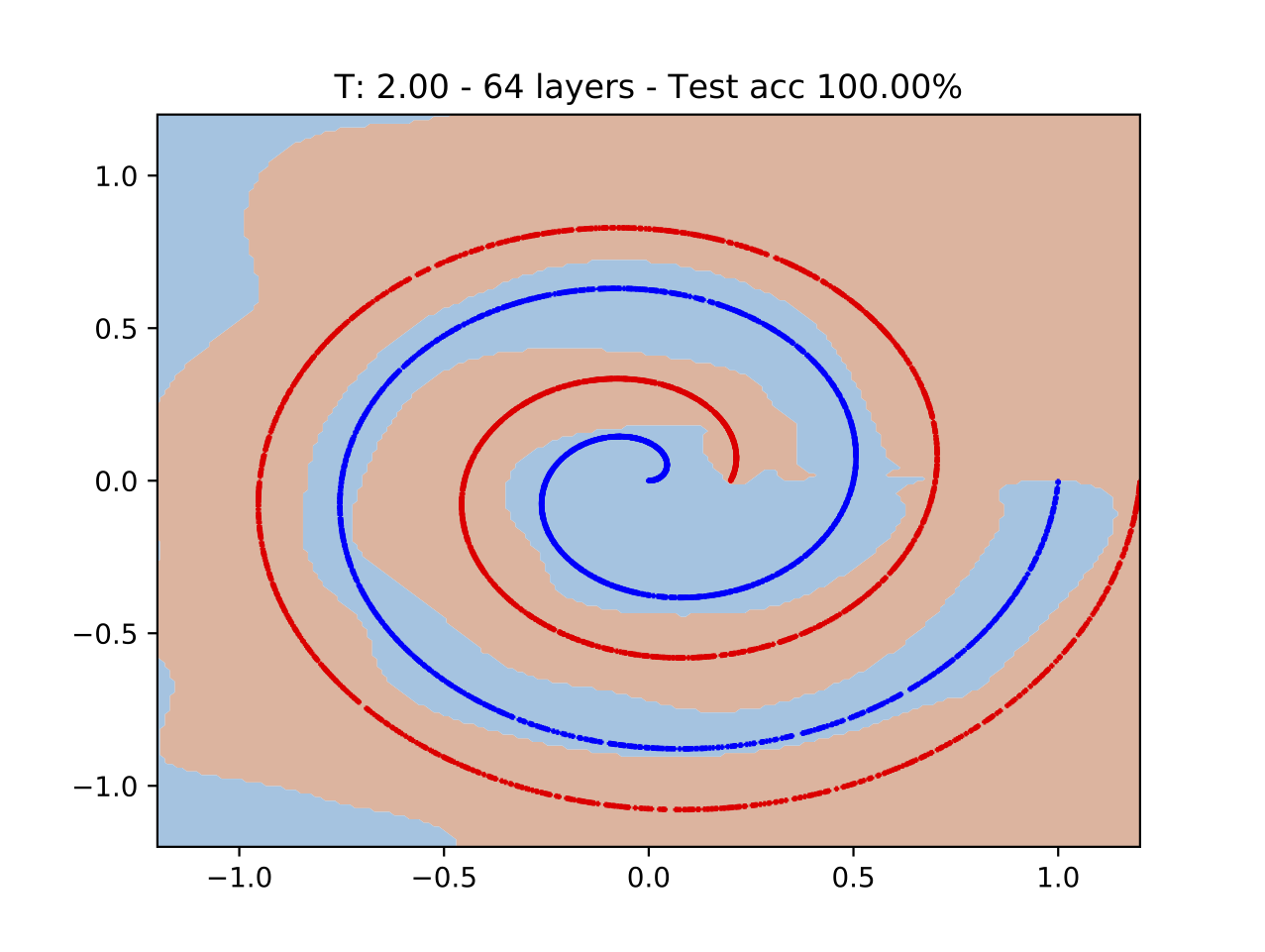
Deep neural networks have become invaluable tools for supervised machine learning, e.g., classification of text or images. While often offering superior results over traditional techniques and successfully expressing complicated patterns in data, deep architectures are known to be challenging to design and train such that they generalize well to new data. Important issues with deep architectures are numerical instabilities in derivative-based learning algorithms commonly called exploding or vanishing gradients. In this paper we propose new forward propagation techniques inspired by systems of Ordinary Differential Equations (ODE) that overcome this challenge and lead to well-posed learning problems for arbitrarily deep networks. The backbone of our approach is our interpretation of deep learning as a parameter estimation problem of nonlinear dynamical systems. Given this formulation, we analyze stability and well-posedness of deep learning and use this new understanding to develop new network architectures. We relate the exploding and vanishing gradient phenomenon to the stability of the discrete ODE and present several strategies for stabilizing deep learning for very deep networks. While our new architectures restrict the solution space, several numerical experiments show their competitiveness with state-of-the-art networks.
PDF Abstract