Stochastic Multiple Target Sampling Gradient Descent
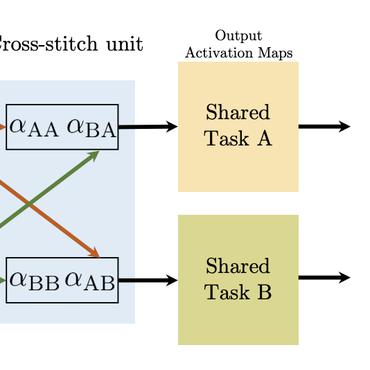
Sampling from an unnormalized target distribution is an essential problem with many applications in probabilistic inference. Stein Variational Gradient Descent (SVGD) has been shown to be a powerful method that iteratively updates a set of particles to approximate the distribution of interest. Furthermore, when analysing its asymptotic properties, SVGD reduces exactly to a single-objective optimization problem and can be viewed as a probabilistic version of this single-objective optimization problem. A natural question then arises: "Can we derive a probabilistic version of the multi-objective optimization?". To answer this question, we propose Stochastic Multiple Target Sampling Gradient Descent (MT-SGD), enabling us to sample from multiple unnormalized target distributions. Specifically, our MT-SGD conducts a flow of intermediate distributions gradually orienting to multiple target distributions, which allows the sampled particles to move to the joint high-likelihood region of the target distributions. Interestingly, the asymptotic analysis shows that our approach reduces exactly to the multiple-gradient descent algorithm for multi-objective optimization, as expected. Finally, we conduct comprehensive experiments to demonstrate the merit of our approach to multi-task learning.
PDF Abstract
Colab
MNIST
CelebA
Fashion-MNIST
MultiMNIST
