Towards Understanding Generalization in Gradient-Based Meta-Learning
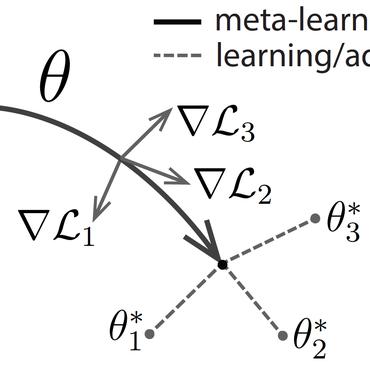
In this work we study generalization of neural networks in gradient-based meta-learning by analyzing various properties of the objective landscapes. We experimentally demonstrate that as meta-training progresses, the meta-test solutions, obtained after adapting the meta-train solution of the model, to new tasks via few steps of gradient-based fine-tuning, become flatter, lower in loss, and further away from the meta-train solution. We also show that those meta-test solutions become flatter even as generalization starts to degrade, thus providing an experimental evidence against the correlation between generalization and flat minima in the paradigm of gradient-based meta-leaning. Furthermore, we provide empirical evidence that generalization to new tasks is correlated with the coherence between their adaptation trajectories in parameter space, measured by the average cosine similarity between task-specific trajectory directions, starting from a same meta-train solution. We also show that coherence of meta-test gradients, measured by the average inner product between the task-specific gradient vectors evaluated at meta-train solution, is also correlated with generalization. Based on these observations, we propose a novel regularizer for MAML and provide experimental evidence for its effectiveness.
PDF Abstract