Unbiased Shape Compactness for Segmentation
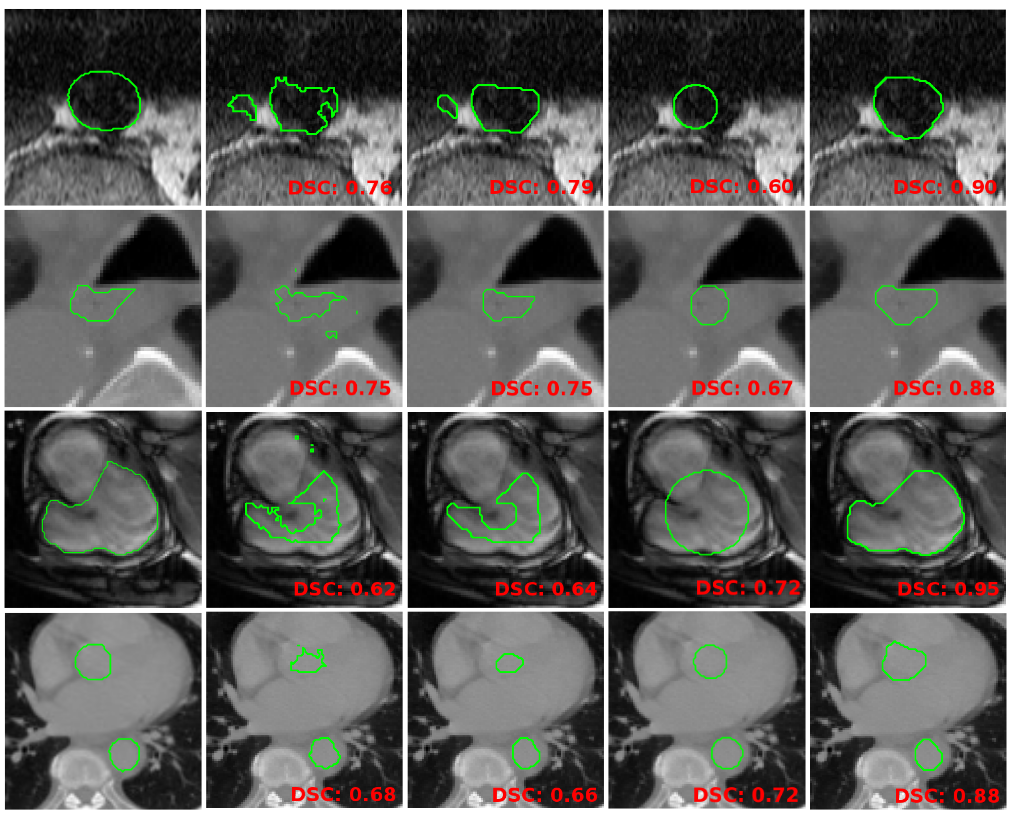
We propose to constrain segmentation functionals with a dimensionless, unbiased and position-independent shape compactness prior, which we solve efficiently with an alternating direction method of multipliers (ADMM). Involving a squared sum of pairwise potentials, our prior results in a challenging high-order optimization problem, which involves dense (fully connected) graphs. We split the problem into a sequence of easier sub-problems, each performed efficiently at each iteration: (i) a sparse-matrix inversion based on Woodbury identity, (ii) a closed-form solution of a cubic equation and (iii) a graph-cut update of a sub-modular pairwise sub-problem with a sparse graph. We deploy our prior in an energy minimization, in conjunction with a supervised classifier term based on CNNs and standard regularization constraints. We demonstrate the usefulness of our energy in several medical applications. In particular, we report comprehensive evaluations of our fully automated algorithm over 40 subjects, showing a competitive performance for the challenging task of abdominal aorta segmentation in MRI.
PDF Abstract