Momentum Rules
Momentum Rules
Demon
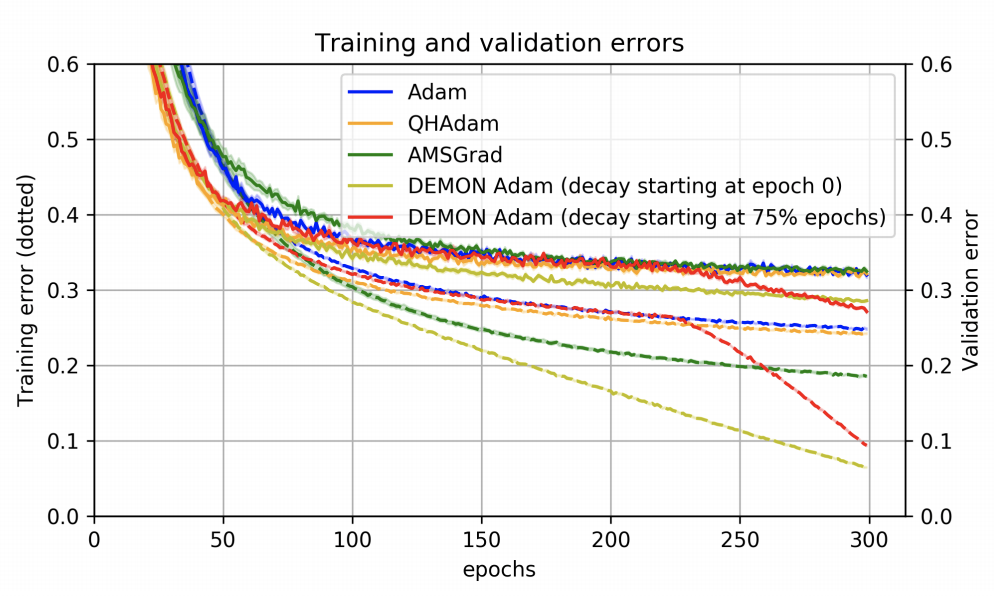
Introduced by Chen et al. in Demon: Improved Neural Network Training with Momentum DecayDecaying Momentum, or Demon, is a stochastic optimizer motivated by decaying the total contribution of a gradient to all future updates. By decaying the momentum parameter, the total contribution of a gradient to all future updates is decayed. A particular gradient term $g_{t}$ contributes a total of $\eta\sum_{i}\beta^{i}$ of its "energy" to all future gradient updates, and this results in the geometric sum, $\sum^{\infty}_{i=1}\beta^{i} = \beta\sum^{\infty}_{i=0}\beta^{i} = \frac{\beta}{\left(1-\beta\right)}$. Decaying this sum results in the Demon algorithm. Letting $\beta_{init}$ be the initial $\beta$; then at the current step $t$ with total $T$ steps, the decay routine is given by solving the below for $\beta_{t}$:
$$ \frac{\beta_{t}}{\left(1-\beta_{t}\right)} = \left(1-t/T\right)\beta_{init}/\left(1-\beta_{init}\right)$$
Where $\left(1-t/T\right)$ refers to the proportion of iterations remaining. Note that Demon typically requires no hyperparameter tuning as it is usually decayed to $0$ or a small negative value at time $T$. Improved performance is observed by delaying the decaying. Demon can be applied to any gradient descent algorithm with a momentum parameter.
Source: Demon: Improved Neural Network Training with Momentum DecayPapers
| Paper | Code | Results | Date | Stars |
|---|
Tasks
| Task | Papers | Share |
|---|---|---|
| Adversarial Attack | 1 | 20.00% |
| Atari Games | 1 | 20.00% |
| Self-Supervised Learning | 1 | 20.00% |
| Pose Estimation | 1 | 20.00% |
| Image Classification | 1 | 20.00% |
Usage Over Time
Components
| Component | Type |
|
|---|---|---|
| 🤖 No Components Found | You can add them if they exist; e.g. Mask R-CNN uses RoIAlign |