Loss Functions
Loss Functions
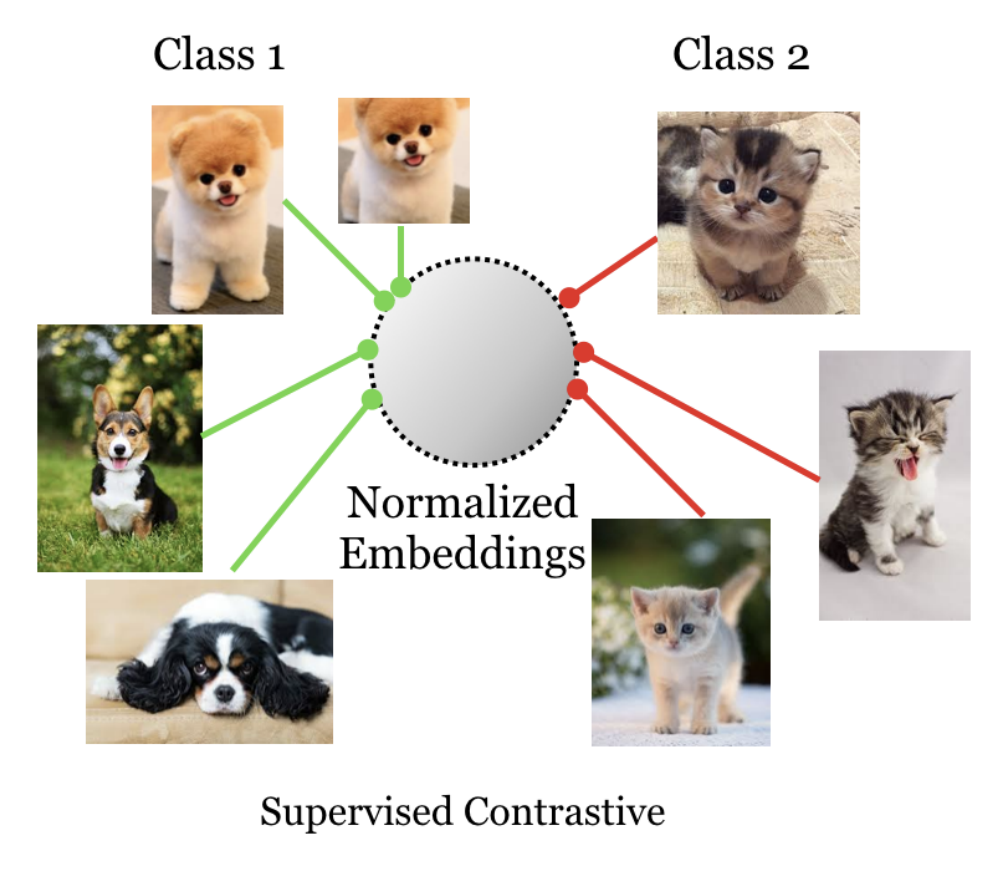
Supervised Contrastive Loss
Introduced by Khosla et al. in Supervised Contrastive LearningSupervised Contrastive Loss is an alternative loss function to cross entropy that the authors argue can leverage label information more effectively. Clusters of points belonging to the same class are pulled together in embedding space, while simultaneously pushing apart clusters of samples from different classes.
$$ \mathcal{L}^{sup}=\sum_{i=1}^{2N}\mathcal{L}_i^{sup} \label{eqn:total_supervised_loss} $$
$$ \mathcal{L}_i^{sup}=\frac{-1}{2N_{\boldsymbol{\tilde{y}}_i}-1}\sum_{j=1}^{2N}\mathbf{1}_{i\neq j}\cdot\mathbf{1}_{\boldsymbol{\tilde{y}}_i=\boldsymbol{\tilde{y}}_j}\cdot\log{\frac{\exp{\left(\boldsymbol{z}_i\cdot\boldsymbol{z}_j/\tau\right)}}{\sum_{k=1}^{2N}\mathbf{1}_{i\neq k}\cdot\exp{\left(\boldsymbol{z}_i\cdot\boldsymbol{z}_k/\tau\right)}}} $$
where $N_{\boldsymbol{\tilde{y}}_i}$ is the total number of images in the minibatch that have the same label, $\boldsymbol{\tilde{y}}_i$, as the anchor, $i$. This loss has important properties well suited for supervised learning: (a) generalization to an arbitrary number of positives, (b) contrastive power increases with more negatives.
Source: Supervised Contrastive LearningPapers
| Paper | Code | Results | Date | Stars |
|---|
Tasks
| Task | Papers | Share |
|---|---|---|
| Image Classification | 10 | 8.47% |
| Long-tail Learning | 5 | 4.24% |
| Classification | 4 | 3.39% |
| Self-Supervised Learning | 4 | 3.39% |
| Semantic Segmentation | 3 | 2.54% |
| Class Incremental Learning | 3 | 2.54% |
| Continual Learning | 3 | 2.54% |
| Domain Adaptation | 2 | 1.69% |
| Fairness | 2 | 1.69% |
Usage Over Time
Components
| Component | Type |
|
|---|---|---|
| 🤖 No Components Found | You can add them if they exist; e.g. Mask R-CNN uses RoIAlign |