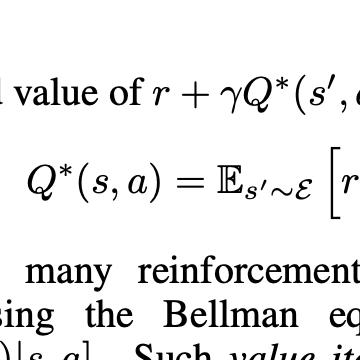A Lyapunov Theory for Finite-Sample Guarantees of Asynchronous Q-Learning and TD-Learning Variants
This paper develops an unified framework to study finite-sample convergence guarantees of a large class of value-based asynchronous reinforcement learning (RL) algorithms. We do this by first reformulating the RL algorithms as \textit{Markovian Stochastic Approximation} (SA) algorithms to solve fixed-point equations. We then develop a Lyapunov analysis and derive mean-square error bounds on the convergence of the Markovian SA. Based on this result, we establish finite-sample mean-square convergence bounds for asynchronous RL algorithms such as $Q$-learning, $n$-step TD, TD$(\lambda)$, and off-policy TD algorithms including V-trace. As a by-product, by analyzing the convergence bounds of $n$-step TD and TD$(\lambda)$, we provide theoretical insights into the bias-variance trade-off, i.e., efficiency of bootstrapping in RL. This was first posed as an open problem in (Sutton, 1999).
PDF Abstract