General $E(2)$-Equivariant Steerable CNNs
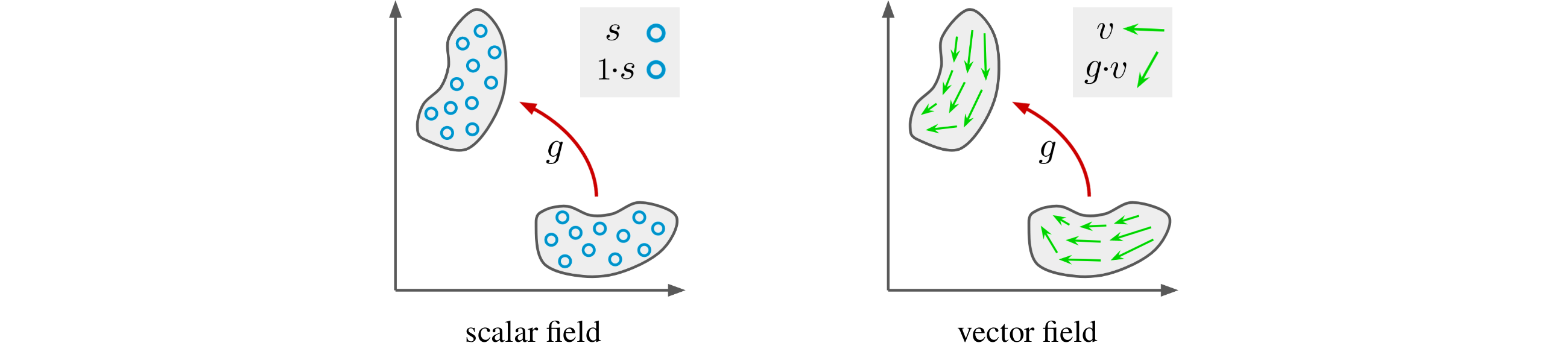
The big empirical success of group equivariant networks has led in recent years to the sprouting of a great variety of equivariant network architectures. A particular focus has thereby been on rotation and reflection equivariant CNNs for planar images. Here we give a general description of $E(2)$-equivariant convolutions in the framework of Steerable CNNs. The theory of Steerable CNNs thereby yields constraints on the convolution kernels which depend on group representations describing the transformation laws of feature spaces. We show that these constraints for arbitrary group representations can be reduced to constraints under irreducible representations. A general solution of the kernel space constraint is given for arbitrary representations of the Euclidean group $E(2)$ and its subgroups. We implement a wide range of previously proposed and entirely new equivariant network architectures and extensively compare their performances. $E(2)$-steerable convolutions are further shown to yield remarkable gains on CIFAR-10, CIFAR-100 and STL-10 when used as a drop-in replacement for non-equivariant convolutions.
PDF AbstractCode
Tasks
Datasets
| Task | Dataset | Model | Metric Name | Metric Value | Global Rank | Benchmark |
|---|---|---|---|---|---|---|
| Image Classification | STL-10 | wrn16/8 D8 D4 D1 | Percentage correct | 90.20 | # 35 | |
| Image Classification | STL-10 | wrn16/8* D8 D4 D1 | Percentage correct | 89.43 | # 39 | |
| Image Classification | STL-10 | wrn16/8 D1 D1 D1 | Percentage correct | 88.83 | # 41 | |
| Image Classification | STL-10 | wrn16/8* D1 D1 D1 | Percentage correct | 88.95 | # 40 | |
| Image Classification | STL-10 | wrn16/8 | Percentage correct | 87.26 | # 47 |



 STL-10
STL-10
