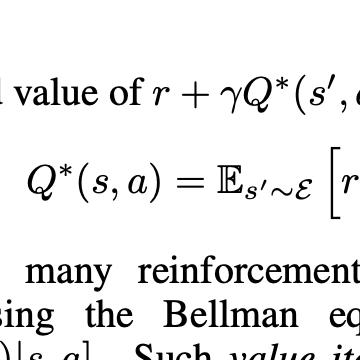Hierarchical Reinforcement Learning with the MAXQ Value Function Decomposition
This paper presents the MAXQ approach to hierarchical reinforcement learning based on decomposing the target Markov decision process (MDP) into a hierarchy of smaller MDPs and decomposing the value function of the target MDP into an additive combination of the value functions of the smaller MDPs. The paper defines the MAXQ hierarchy, proves formal results on its representational power, and establishes five conditions for the safe use of state abstractions. The paper presents an online model-free learning algorithm, MAXQ-Q, and proves that it converges wih probability 1 to a kind of locally-optimal policy known as a recursively optimal policy, even in the presence of the five kinds of state abstraction. The paper evaluates the MAXQ representation and MAXQ-Q through a series of experiments in three domains and shows experimentally that MAXQ-Q (with state abstractions) converges to a recursively optimal policy much faster than flat Q learning. The fact that MAXQ learns a representation of the value function has an important benefit: it makes it possible to compute and execute an improved, non-hierarchical policy via a procedure similar to the policy improvement step of policy iteration. The paper demonstrates the effectiveness of this non-hierarchical execution experimentally. Finally, the paper concludes with a comparison to related work and a discussion of the design tradeoffs in hierarchical reinforcement learning.
PDF Abstract