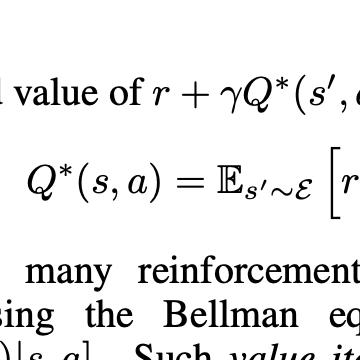Instance-optimality in optimal value estimation: Adaptivity via variance-reduced Q-learning
Various algorithms in reinforcement learning exhibit dramatic variability in their convergence rates and ultimate accuracy as a function of the problem structure. Such instance-specific behavior is not captured by existing global minimax bounds, which are worst-case in nature. We analyze the problem of estimating optimal $Q$-value functions for a discounted Markov decision process with discrete states and actions and identify an instance-dependent functional that controls the difficulty of estimation in the $\ell_\infty$-norm. Using a local minimax framework, we show that this functional arises in lower bounds on the accuracy on any estimation procedure. In the other direction, we establish the sharpness of our lower bounds, up to factors logarithmic in the state and action spaces, by analyzing a variance-reduced version of $Q$-learning. Our theory provides a precise way of distinguishing "easy" problems from "hard" ones in the context of $Q$-learning, as illustrated by an ensemble with a continuum of difficulty.
PDF Abstract