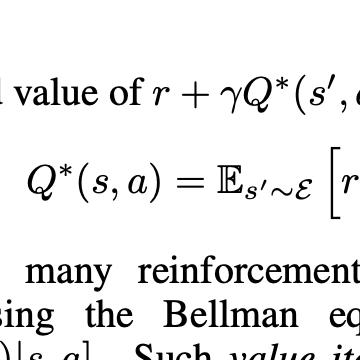Maximizing Influence with Graph Neural Networks
Finding the seed set that maximizes the influence spread over a network is a well-known NP-hard problem. Though a greedy algorithm can provide near-optimal solutions, the subproblem of influence estimation renders the solutions inefficient. In this work, we propose \textsc{Glie}, a graph neural network that learns how to estimate the influence spread of the independent cascade. \textsc{Glie} relies on a theoretical upper bound that is tightened through supervised training. Experiments indicate that it provides accurate influence estimation for real graphs up to 10 times larger than the train set. Subsequently, we incorporate it into two influence maximization techniques. We first utilize Cost Effective Lazy Forward optimization substituting Monte Carlo simulations with \textsc{Glie}, surpassing the benchmarks albeit with a computational overhead. To improve computational efficiency we develop a provably submodular influence spread based on \textsc{Glie}'s representations, to rank nodes while building the seed set adaptively. The proposed algorithms are inductive, meaning they are trained on graphs with less than 300 nodes and up to 5 seeds, and tested on graphs with millions of nodes and up to 200 seeds. The final method exhibits the most promising combination of time efficiency and influence quality, outperforming several baselines.
PDF Abstract