On the Stability of a non-hyperbolic nonlinear map with non-bounded set of non-isolated fixed points with applications to Machine Learning
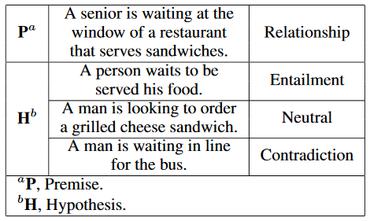
This paper deals with the convergence analysis of the SUCPA (Semi Unsupervised Calibration through Prior Adaptation) algorithm, defined from a first-order non-linear difference equations, first developed to correct the scores output by a supervised machine learning classifier. The convergence analysis is addressed as a dynamical system problem, by studying the local and global stability of the nonlinear map derived from the algorithm. This map, which is defined by a composition of exponential and rational functions, turns out to be non-hyperbolic with a non-bounded set of non-isolated fixed points. Hence, a non-standard method for solving the convergence analysis is used consisting of an ad-hoc geometrical approach. For a binary classification problem (two-dimensional map), we rigorously prove that the map is globally asymptotically stable. Numerical experiments on real-world application are performed to support the theoretical results by means of two different classification problems: Sentiment Polarity performed with a Large Language Model and Cat-Dog Image classification. For a greater number of classes, the numerical evidence shows the same behavior of the algorithm, and this is illustrated with a Natural Language Inference example. The experiment codes are publicly accessible online at the following repository: https://github.com/LautaroEst/sucpa-convergence
PDF Abstract