 Position Embeddings
Position Embeddings
Absolute Position Encodings
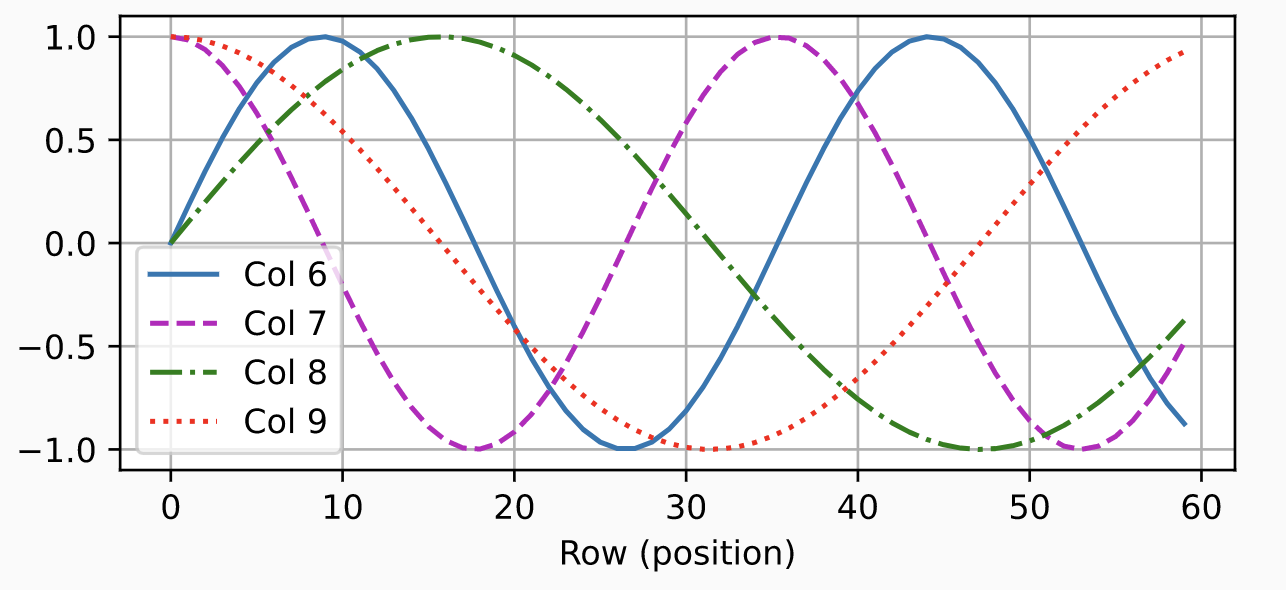
Introduced by Vaswani et al. in Attention Is All You NeedAbsolute Position Encodings are a type of position embeddings for [Transformer-based models] where positional encodings are added to the input embeddings at the bottoms of the encoder and decoder stacks. The positional encodings have the same dimension $d_{model}$ as the embeddings, so that the two can be summed. In the original implementation, sine and cosine functions of different frequencies are used:
$$ \text{PE}\left(pos, 2i\right) = \sin\left(pos/10000^{2i/d_{model}}\right) $$
$$ \text{PE}\left(pos, 2i+1\right) = \cos\left(pos/10000^{2i/d_{model}}\right) $$
where $pos$ is the position and $i$ is the dimension. That is, each dimension of the positional encoding corresponds to a sinusoid. The wavelengths form a geometric progression from $2\pi$ to $10000 \dot 2\pi$. This function was chosen because the authors hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset $k$, $\text{PE}_{pos+k}$ can be represented as a linear function of $\text{PE}_{pos}$.
Image Source: D2L.ai
Source: Attention Is All You NeedPapers
| Paper | Code | Results | Date | Stars |
|---|
Tasks
| Task | Papers | Share |
|---|---|---|
| Language Modelling | 47 | 6.57% |
| Semantic Segmentation | 28 | 3.92% |
| Large Language Model | 21 | 2.94% |
| Question Answering | 20 | 2.80% |
| Object Detection | 18 | 2.52% |
| In-Context Learning | 15 | 2.10% |
| Image Classification | 12 | 1.68% |
| Denoising | 12 | 1.68% |
| Retrieval | 12 | 1.68% |
 3D Dynamic Scene Graph
3D Dynamic Scene Graph