Normalization
Normalization
Conditional Batch Normalization
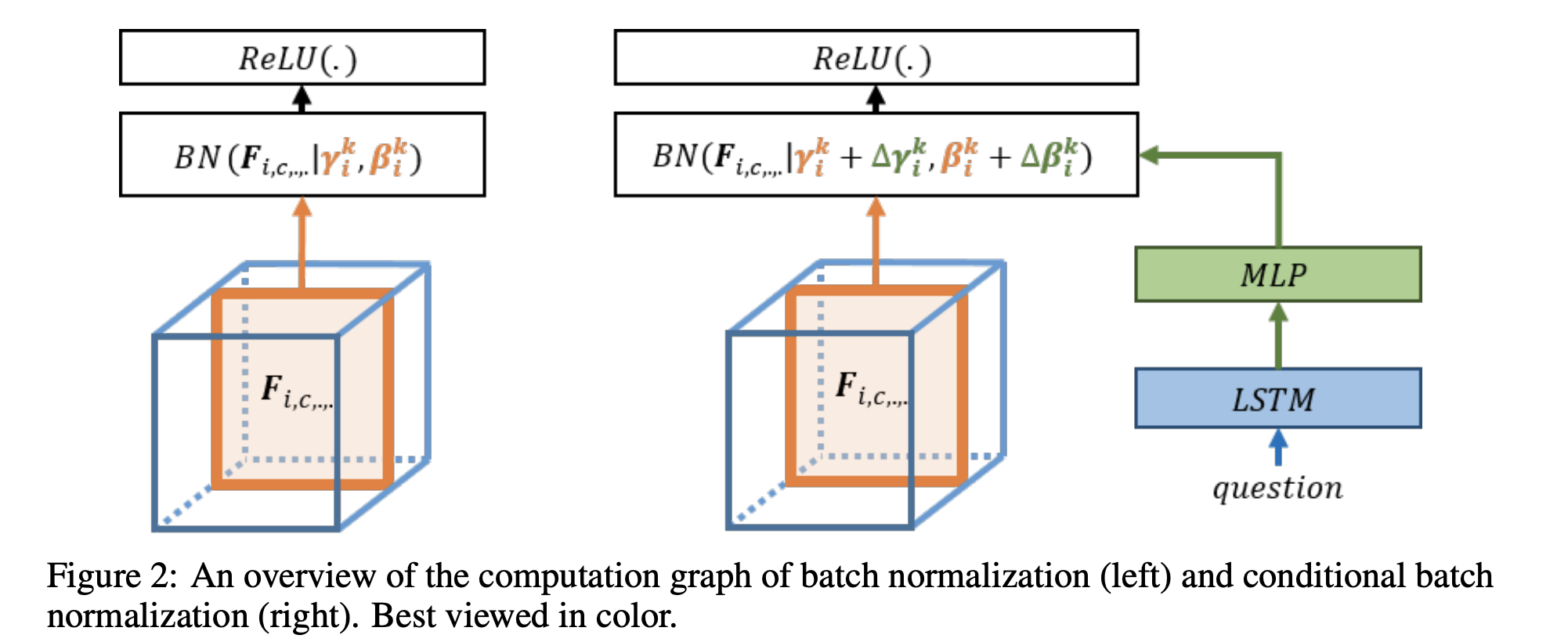
Introduced by Vries et al. in Modulating early visual processing by languageConditional Batch Normalization (CBN) is a class-conditional variant of batch normalization. The key idea is to predict the $\gamma$ and $\beta$ of the batch normalization from an embedding - e.g. a language embedding in VQA. CBN enables the linguistic embedding to manipulate entire feature maps by scaling them up or down, negating them, or shutting them off. CBN has also been used in GANs to allow class information to affect the batch normalization parameters.
Consider a single convolutional layer with batch normalization module $\text{BN}\left(F_{i,c,h,w}|\gamma_{c}, \beta_{c}\right)$ for which pretrained scalars $\gamma_{c}$ and $\beta_{c}$ are available. We would like to directly predict these affine scaling parameters from, e.g., a language embedding $\mathbf{e_{q}}$. When starting the training procedure, these parameters must be close to the pretrained values to recover the original ResNet model as a poor initialization could significantly deteriorate performance. Unfortunately, it is difficult to initialize a network to output the pretrained $\gamma$ and $\beta$. For these reasons, the authors propose to predict a change $\delta\beta_{c}$ and $\delta\gamma_{c}$ on the frozen original scalars, for which it is straightforward to initialize a neural network to produce an output with zero-mean and small variance.
The authors use a one-hidden-layer MLP to predict these deltas from a question embedding $\mathbf{e_{q}}$ for all feature maps within the layer:
$$\Delta\beta = \text{MLP}\left(\mathbf{e_{q}}\right)$$
$$\Delta\gamma = \text{MLP}\left(\mathbf{e_{q}}\right)$$
So, given a feature map with $C$ channels, these MLPs output a vector of size $C$. We then add these predictions to the $\beta$ and $\gamma$ parameters:
$$ \hat{\beta}_{c} = \beta_{c} + \Delta\beta_{c} $$
$$ \hat{\gamma}_{c} = \gamma_{c} + \Delta\gamma_{c} $$
Finally, these updated $\hat{β}$ and $\hat{\gamma}$ are used as parameters for the batch normalization: $\text{BN}\left(F_{i,c,h,w}|\hat{\gamma_{c}}, \hat{\beta_{c}}\right)$. The authors freeze all ResNet parameters, including $\gamma$ and $\beta$, during training. A ResNet consists of four stages of computation, each subdivided in several residual blocks. In each block, the authors apply CBN to the three convolutional layers.
Source: Modulating early visual processing by languagePapers
| Paper | Code | Results | Date | Stars |
|---|
Tasks
| Task | Papers | Share |
|---|---|---|
| Image Generation | 40 | 19.32% |
| Conditional Image Generation | 16 | 7.73% |
| Multi-agent Reinforcement Learning | 7 | 3.38% |
| Super-Resolution | 6 | 2.90% |
| Reinforcement Learning (RL) | 6 | 2.90% |
| Decision Making | 5 | 2.42% |
| Denoising | 4 | 1.93% |
| Clustering | 4 | 1.93% |
| Benchmarking | 3 | 1.45% |
Usage Over Time
Components
| Component | Type |
|
|---|---|---|
 Batch Normalization
Batch Normalization
|
Normalization | |
 Feedforward Network
Feedforward Network
|
Feedforward Networks |