Generalized Linear Models
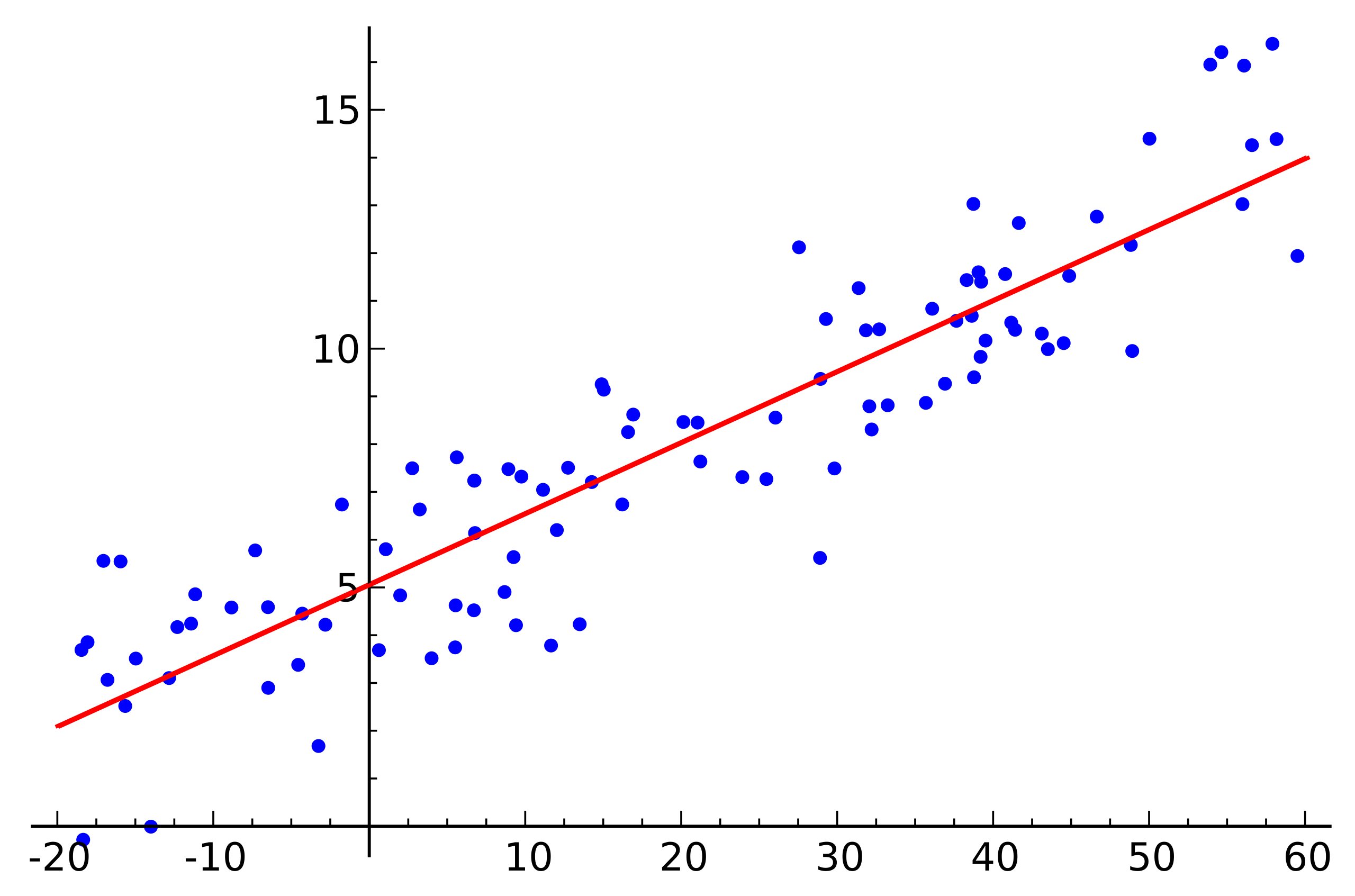
Linear Regression
Linear Regression is a method for modelling a relationship between a dependent variable and independent variables. These models can be fit with numerous approaches. The most common is least squares, where we minimize the mean square error between the predicted values $\hat{y} = \textbf{X}\hat{\beta}$ and actual values $y$: $\left(y-\textbf{X}\beta\right)^{2}$.
We can also define the problem in probabilistic terms as a generalized linear model (GLM) where the pdf is a Gaussian distribution, and then perform maximum likelihood estimation to estimate $\hat{\beta}$.
Image Source: Wikipedia
Papers
| Paper | Code | Results | Date | Stars |
|---|
Tasks
| Task | Papers | Share |
|---|---|---|
| In-Context Learning | 21 | 6.12% |
| Decision Making | 11 | 3.21% |
| Uncertainty Quantification | 10 | 2.92% |
| Causal Inference | 9 | 2.62% |
| Continual Learning | 9 | 2.62% |
| Management | 9 | 2.62% |
| Federated Learning | 9 | 2.62% |
| Time Series Analysis | 9 | 2.62% |
| Variable Selection | 8 | 2.33% |
Usage Over Time
Components
| Component | Type |
|
|---|---|---|
| 🤖 No Components Found | You can add them if they exist; e.g. Mask R-CNN uses RoIAlign |
