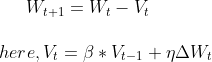Stochastic Optimization
Stochastic Optimization
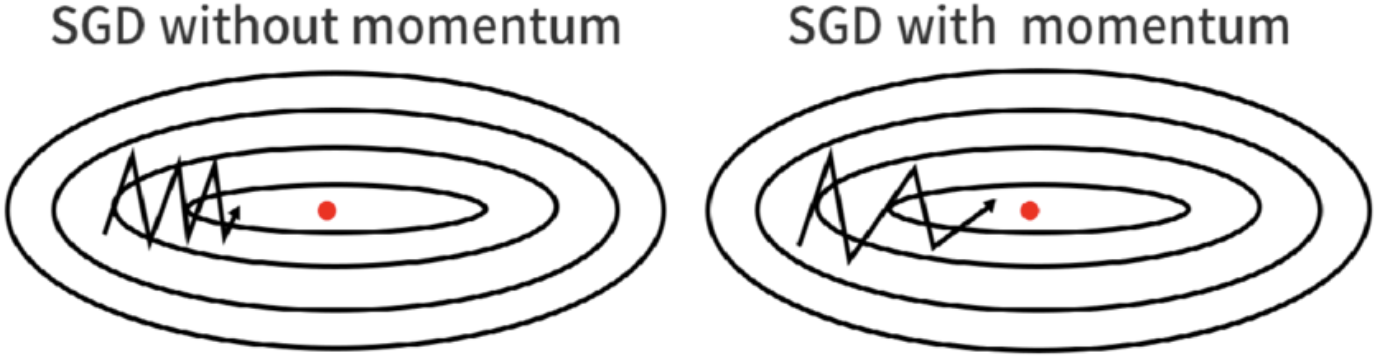
SGD with Momentum
Why SGD with Momentum?
In deep learning, we have used stochastic gradient descent as one of the optimizers because at the end we will find the minimum weight and bias at which the model loss is lowest. In the SGD we have some issues in which the SGD does not work perfectly because in deep learning we got a non-convex cost function graph and if use the simple SGD then it leads to low performance. There are 3 main reasons why it does not work:
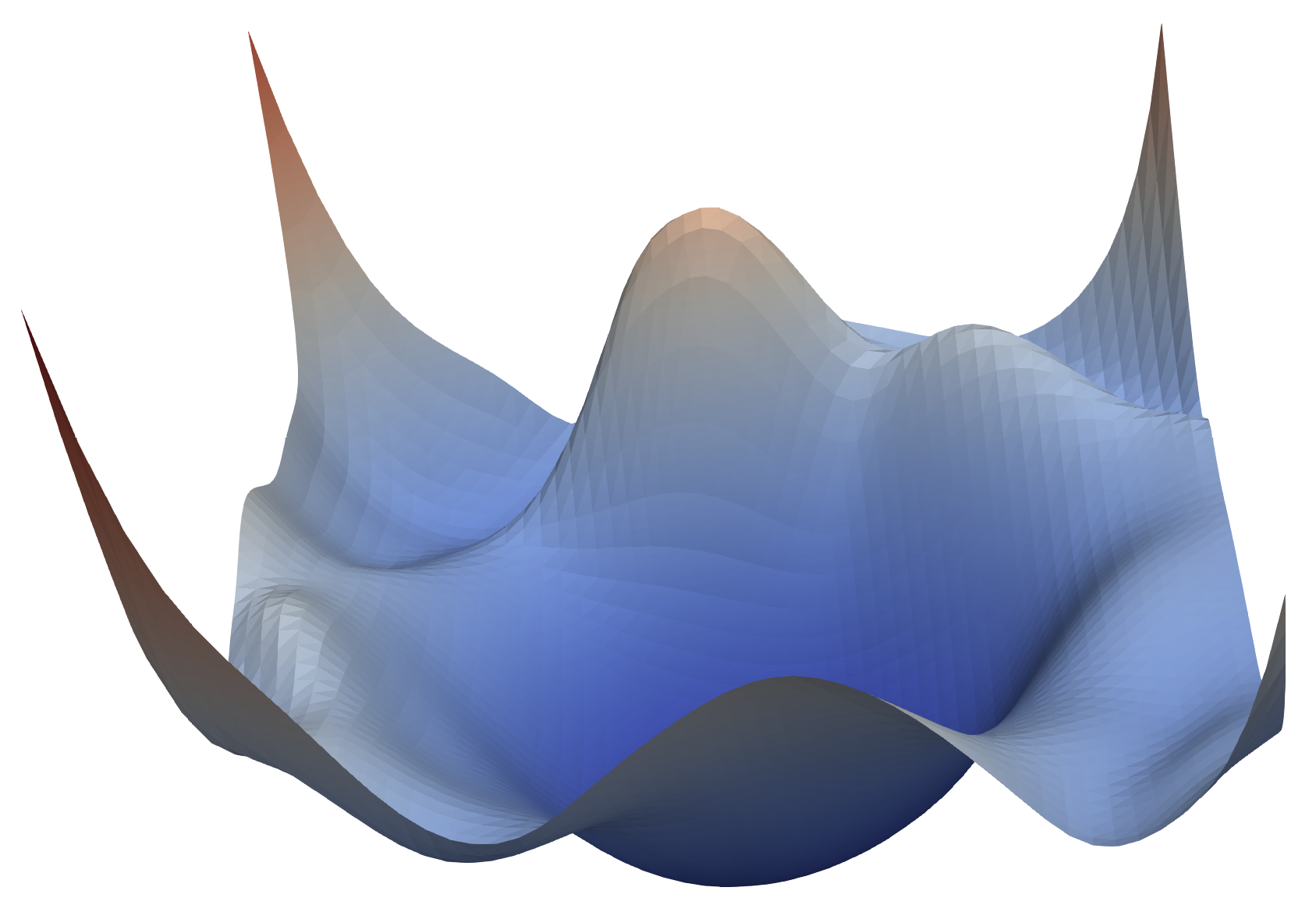
1) We end up in local minima and not able to reach global minima At the start, we randomly start at some point and we are going to end up at the local minimum and not able to reach the global minimum.
2) Saddle Point will be the stop for reaching global minima A saddle point is a point where in one direction the surface goes in the upward direction and in another direction it goes downwards. So that the slope is changing very gradually so the speed of changing is going to slow and as result, the training also going to slow.
3) High curvature can be a reason The larger radius leads to low curvature and vice-versa. It will be difficult to traverse in the large curvature which was generally high in non-convex optimization. By using the SGD with Momentum optimizer we can overcome the problems like high curvature, consistent gradient, and noisy gradient.
What is SGD with Momentum?
SGD with Momentum is one of the optimizers which is used to improve the performance of the neural network.
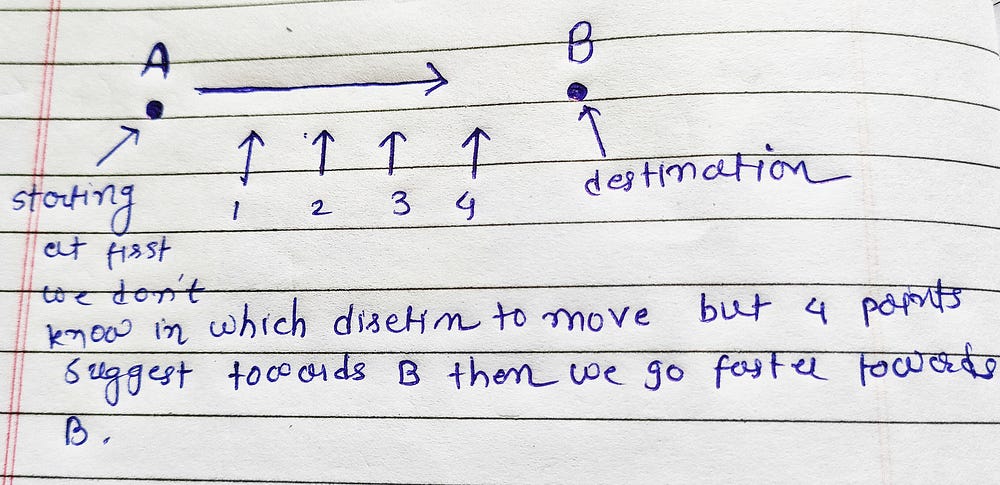
Let's take an example and understand the intuition behind the optimizer suppose we have a ball which is sliding from the start of the slope as it goes the speed of the bowl is increased over time. If we have one point A and we want to reach point B and we don't know in which direction to move but we ask for the 4 points which have already reached point B. If all 4 points are pointing you in the same direction then the confidence of the A is more and it goes in the direction pointed very fast. This is the main concept behind the SGD with Momentum.
How does SGD with Momentum work?
So first to understand the concept of exponentially weighted moving average (EWMA). It was a technique through which try to find the trend in time series data. The formula of the EWMA is :
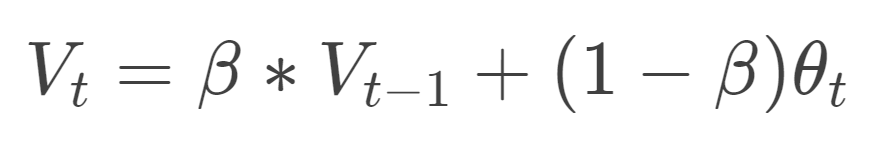
In the formula, β represents the weightage that is going to assign to the past values of the gradient. The values of β is from 0 < β < 1. If the value of the beta is 0.5 then it means that the 1/1–0.5 = 2 so it represents that the calculated average was from the previous 2 readings.
The value of Vt depends on β. The higher the value of β the more we try to get an average of more past data and vice-versa. For example, let's take the value of β 0.98 and 0.5 for two different scenarios so if we do 1/1-β then we get 50 and 10 respectively so it was clear that to calculate the average we take past 50 and 10 outcomes respectively for both cases. Now in SGD with Momentum, we use the same concept of EWMA. Here we introduce the term velocity v which is used to denote the change in the gradient to get to the global minima. The change in the weights is denoted by the formula:
the β part of the V formula denotes and is useful to compute the confidence or we can say the past velocity for calculating Vt we have to calculate Vt-1 and for calculating Vt-1 we have to calculate Vt-2 and likewise. So we are using the history of velocity to calculate the momentum and this is the part that provides acceleration to the formula.
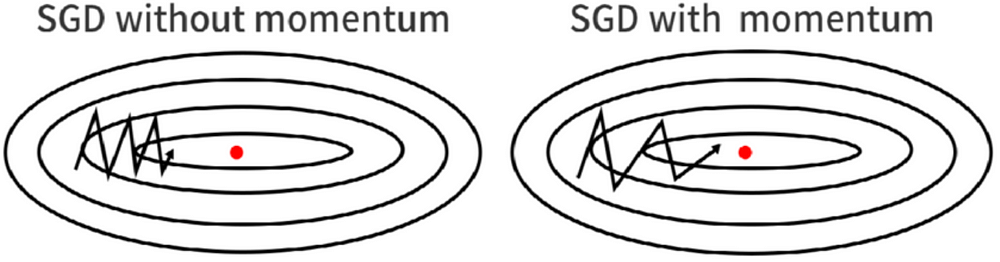
Here we have to consider two cases: 1. β=0 then, as per the formula weight updating is going to just work as a Stochastic gradient descent. Here we called β a decaying factor because it is defining the speed of past velocity.
- β=1 then, there will be no decay. It involves the dynamic equilibrium which is not desired so we generally use the value of β like 0.9,0.99or 0.5 only.
Advantages of SGD with Momentum :
- Momentum is faster than stochastic gradient descent the training will be faster than SGD.
- Local minima can be an escape and reach global minima due to the momentum involved.
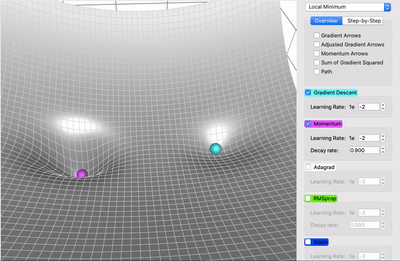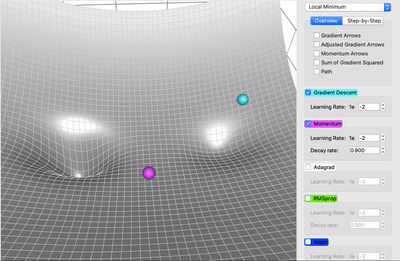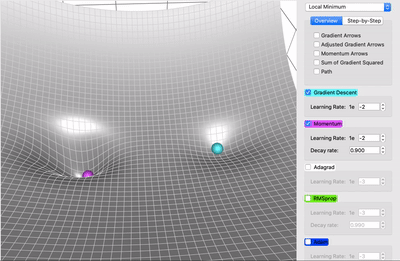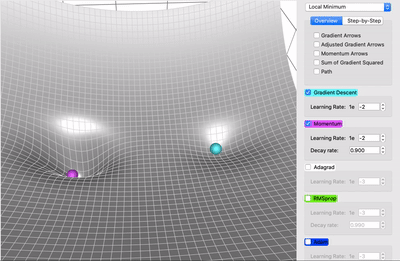
Here in the video, we can see that purple is SGD with Momentum and light blue is for SGD the SGD with Momentum can reach global minima whereas SGD is stuck in local minima. But there is a catch, the momentum itself can be a problem sometimes because of the high momentum after reaching global minima it is still fluctuating and take some time to get stable at global minima. And that kind of behavior leads to time consumption which makes SGD with Momentum slower than other optimization out there but still faster than SGD.
Papers
| Paper | Code | Results | Date | Stars |
|---|
Tasks
| Task | Papers | Share |
|---|---|---|
| Image Classification | 63 | 19.27% |
| Object Detection | 49 | 14.98% |
| General Classification | 24 | 7.34% |
| Semantic Segmentation | 23 | 7.03% |
| Instance Segmentation | 14 | 4.28% |
| Real-Time Object Detection | 10 | 3.06% |
| Classification | 7 | 2.14% |
| Image Segmentation | 6 | 1.83% |
| Domain Generalization | 5 | 1.53% |
Usage Over Time
Components
| Component | Type |
|
|---|---|---|
| 🤖 No Components Found | You can add them if they exist; e.g. Mask R-CNN uses RoIAlign |