Stochastic Optimization
Stochastic Optimization
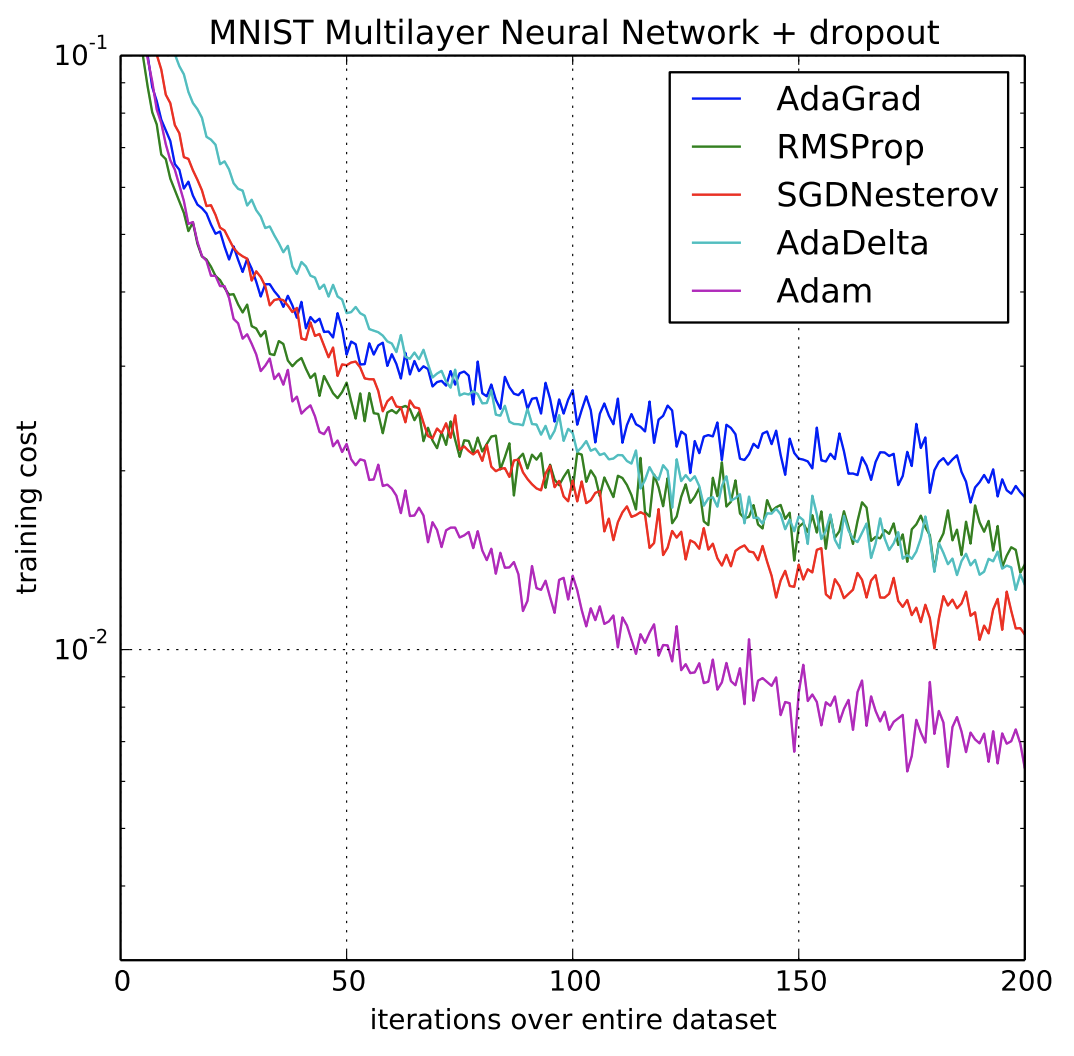
Adam
Introduced by Kingma et al. in Adam: A Method for Stochastic OptimizationAdam is an adaptive learning rate optimization algorithm that utilises both momentum and scaling, combining the benefits of RMSProp and SGD w/th Momentum. The optimizer is designed to be appropriate for non-stationary objectives and problems with very noisy and/or sparse gradients.
The weight updates are performed as:
$$ w_{t} = w_{t-1} - \eta\frac{\hat{m}_{t}}{\sqrt{\hat{v}_{t}} + \epsilon} $$
with
$$ \hat{m}_{t} = \frac{m_{t}}{1-\beta^{t}_{1}} $$
$$ \hat{v}_{t} = \frac{v_{t}}{1-\beta^{t}_{2}} $$
$$ m_{t} = \beta_{1}m_{t-1} + (1-\beta_{1})g_{t} $$
$$ v_{t} = \beta_{2}v_{t-1} + (1-\beta_{2})g_{t}^{2} $$
$ \eta $ is the step size/learning rate, around 1e-3 in the original paper. $ \epsilon $ is a small number, typically 1e-8 or 1e-10, to prevent dividing by zero. $ \beta_{1} $ and $ \beta_{2} $ are forgetting parameters, with typical values 0.9 and 0.999, respectively.
Source: Adam: A Method for Stochastic OptimizationPapers
| Paper | Code | Results | Date | Stars |
|---|
Tasks
| Task | Papers | Share |
|---|---|---|
| Language Modelling | 56 | 7.70% |
| Retrieval | 36 | 4.95% |
| Question Answering | 27 | 3.71% |
| Large Language Model | 26 | 3.58% |
| Semantic Segmentation | 20 | 2.75% |
| Sentence | 14 | 1.93% |
| Object Detection | 13 | 1.79% |
| Image Classification | 12 | 1.65% |
| Benchmarking | 11 | 1.51% |
Usage Over Time
Components
| Component | Type |
|
|---|---|---|
| 🤖 No Components Found | You can add them if they exist; e.g. Mask R-CNN uses RoIAlign |