Change Detection in Graph Streams by Learning Graph Embeddings on Constant-Curvature Manifolds
The space of graphs is often characterised by a non-trivial geometry, which complicates learning and inference in practical applications. A common approach is to use embedding techniques to represent graphs as points in a conventional Euclidean space, but non-Euclidean spaces have often been shown to be better suited for embedding graphs. Among these, constant-curvature Riemannian manifolds (CCMs) offer embedding spaces suitable for studying the statistical properties of a graph distribution, as they provide ways to easily compute metric geodesic distances. In this paper, we focus on the problem of detecting changes in stationarity in a stream of attributed graphs. To this end, we introduce a novel change detection framework based on neural networks and CCMs, that takes into account the non-Euclidean nature of graphs. Our contribution in this work is twofold. First, via a novel approach based on adversarial learning, we compute graph embeddings by training an autoencoder to represent graphs on CCMs. Second, we introduce two novel change detection tests operating on CCMs. We perform experiments on synthetic data, as well as two real-world application scenarios: the detection of epileptic seizures using functional connectivity brain networks, and the detection of hostility between two subjects, using human skeletal graphs. Results show that the proposed methods are able to detect even small changes in a graph-generating process, consistently outperforming approaches based on Euclidean embeddings.
PDF Abstract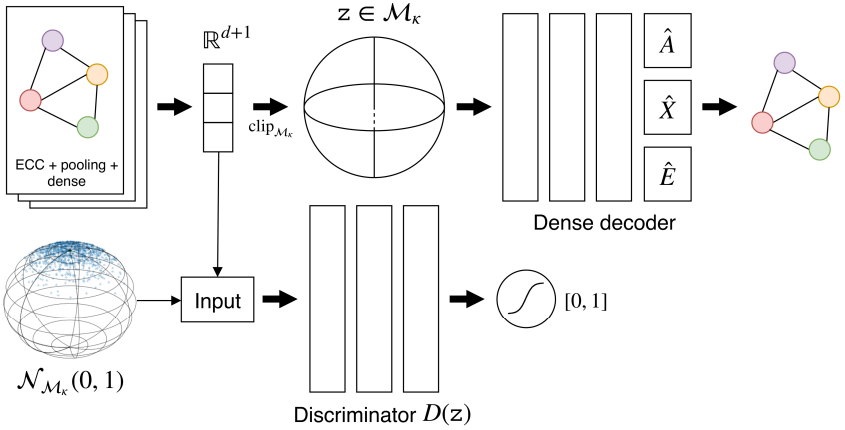


 NTU RGB+D
NTU RGB+D