Directional Graph Networks
The lack of anisotropic kernels in graph neural networks (GNNs) strongly limits their expressiveness, contributing to well-known issues such as over-smoothing. To overcome this limitation, we propose the first globally consistent anisotropic kernels for GNNs, allowing for graph convolutions that are defined according to topologicaly-derived directional flows. First, by defining a vector field in the graph, we develop a method of applying directional derivatives and smoothing by projecting node-specific messages into the field. Then, we propose the use of the Laplacian eigenvectors as such vector field. We show that the method generalizes CNNs on an $n$-dimensional grid and is provably more discriminative than standard GNNs regarding the Weisfeiler-Lehman 1-WL test. We evaluate our method on different standard benchmarks and see a relative error reduction of 8% on the CIFAR10 graph dataset and 11% to 32% on the molecular ZINC dataset, and a relative increase in precision of 1.6% on the MolPCBA dataset. An important outcome of this work is that it enables graph networks to embed directions in an unsupervised way, thus allowing a better representation of the anisotropic features in different physical or biological problems.
PDF Abstract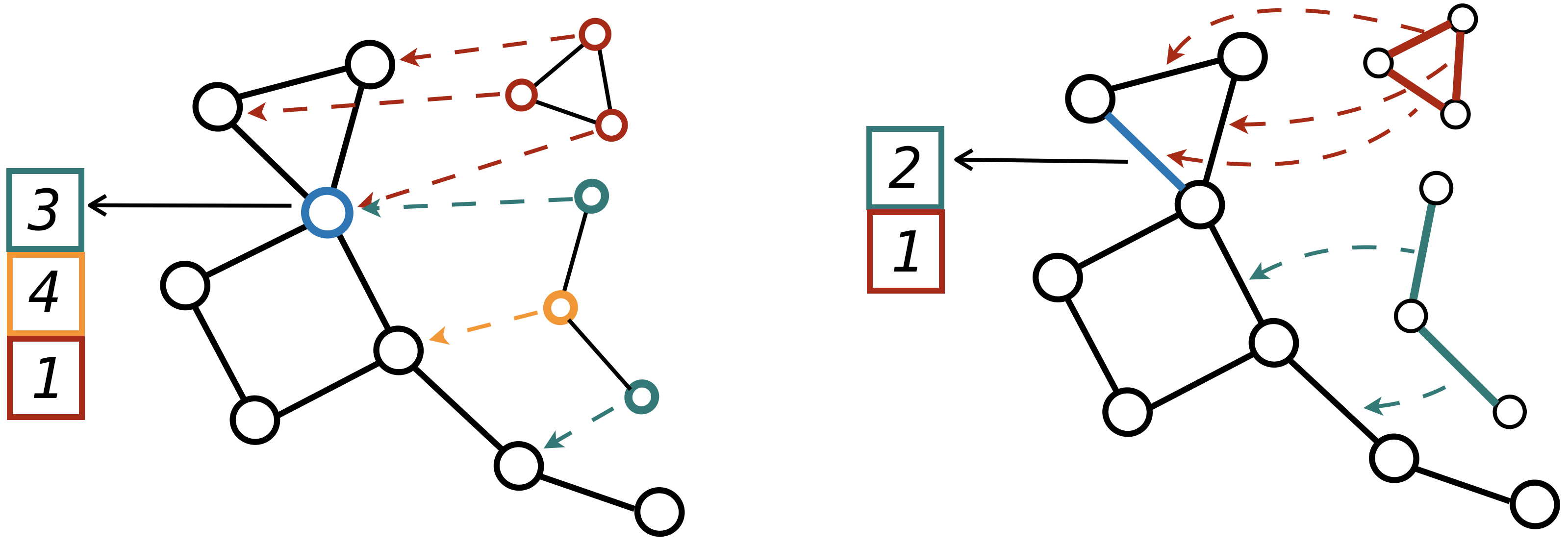









 CIFAR-10
CIFAR-10
 OGB
OGB
